Toán rời rạc là gì? 3 chủ đề phổ biến của Toán rời rạc

1. Toán rời rạc là gì?

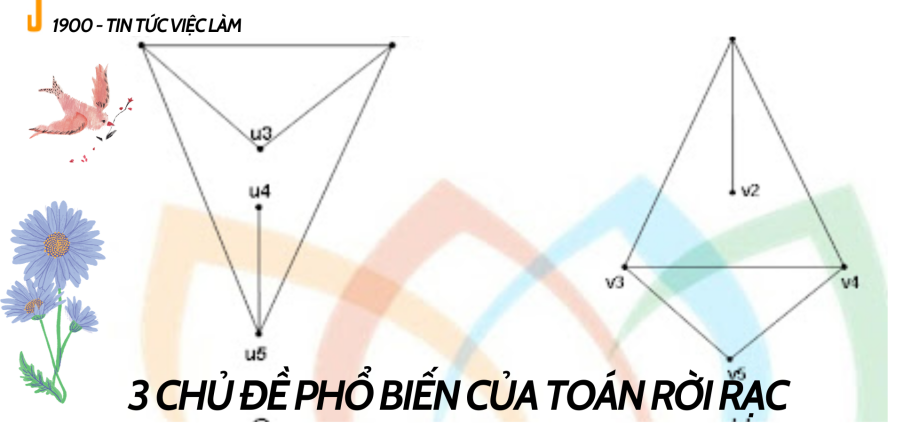
Toán rời rạc là nền tảng của thuật toán và nhiều mô hình học quan trọng trong máy tính như logic, số bool, lý thuyết đồ thị, xác suất, tổ hợp,… Đây là nền toán học quan trọng của máy tính, nếu trở thành lập trình viên, bạn sẽ ước gì mình được học toán rời rạc sâu hơn. Tùy hướng mà bạn có thể đi lựa chọn thời gian đầu thích hợp để học môn này.

Bộ môn toán học này còn được gọi là Discrete mathematics là một lĩnh vực nghiên cứu và xử lý các đối tượng trong toán rời rạc. Đó là một trong những yếu tố làm Toán rời rạc trở nên quan trọng là việc lưu trữ, xử lý thông tin trong các hệ thống máy tính về bản chất rời rạc.

Đọc thêm: Top việc làm đang tuyển dụng mới nhất năm 2024

2. 3 chủ đề phổ biến của toán học rời rạc

Toán rời rạc là một lĩnh vực của toán học nghiên cứu chi tiết về các đối tượng rời rạc. Mọi người sẽ sử dụng công cụ của Discrete mathematics khi đếm các đối tượng. Khi nghiên cứu quan sát giữa các tệp rời rạc, một trong những nguyên nhân chủ yếu làm nâng tầm quan trọng của Discrete mathematics. Khi học toán rời rạc, bạn cần học qua các phần sau:

Trình bày các vấn đề lý thuyết tổ hợp

Ở phần này, bạn sẽ được học xoay quanh 4 bài toán cơ bản như các bài toán đếm, các bài toán tồn tại, các bài toán liệt kê và các bài toán tối ưu tổ hợp. Nội dung của Phần I không những nâng cao tư duy toán mà còn giúp bạn làm quen với tư duy thuật toán trong việc giải quyết các vấn đề trong thực tế, đồng thời cũng rèn luyện kỹ thuật lập trình tất cả các bài toán tổ hợp.

Đề cập đến lý thuyết của đồ thị

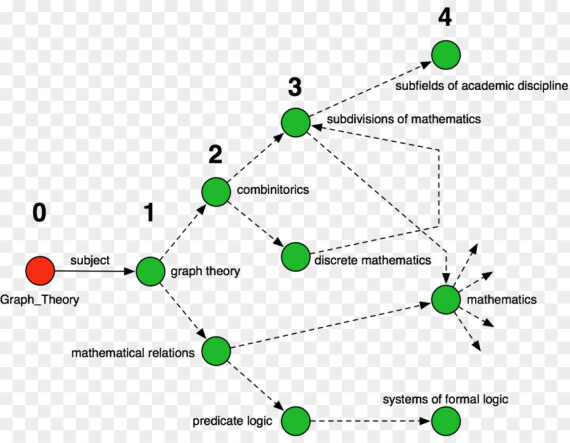
Đề cập đến lý thuyết của đồ thị, một cấu trúc rời rạc tìm được những ứng dụng rộng rãi trong lĩnh vực khoa học kỹ thuật và đời sống. Trong phần này, mọi người sẽ được học các khái niệm cơ bản, các bài toán ứng dụng quan trọng của lý thuyết đồ thị.

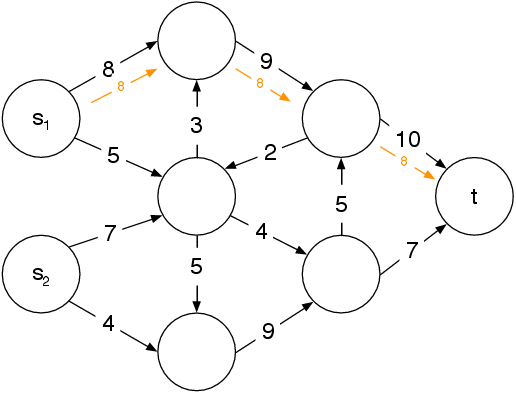
Những bài toán Discrete mathematics đó bao gồm: Bài toán cây khung nhỏ, Bài toán đường đi ngắn nhất hoặc bài toán luồng cực đại trong mạng…Những thuật toán này dùng để giải quyết những chương trình cài đặt chương trình trên máy tính.

Lý thuyết hàm đại số logic

Cuối cùng, bạn sẽ được học các lý thuyết liên quan đến đại số logic, ở phần này sẽ giúp bạn nắm bắt những vấn đề phức tạp của kỹ thuật máy tính. Sau phần trình bày các khái niệm cơ bản, phần này sẽ đi sâu vào vấn đề tối thiểu hóa của các hàm đại số logic và mô tả một số thuật toán quan trọng.

 Ví dụ: Bài toán ghép cặp sao cho không xảy ra tắc nghẽn :

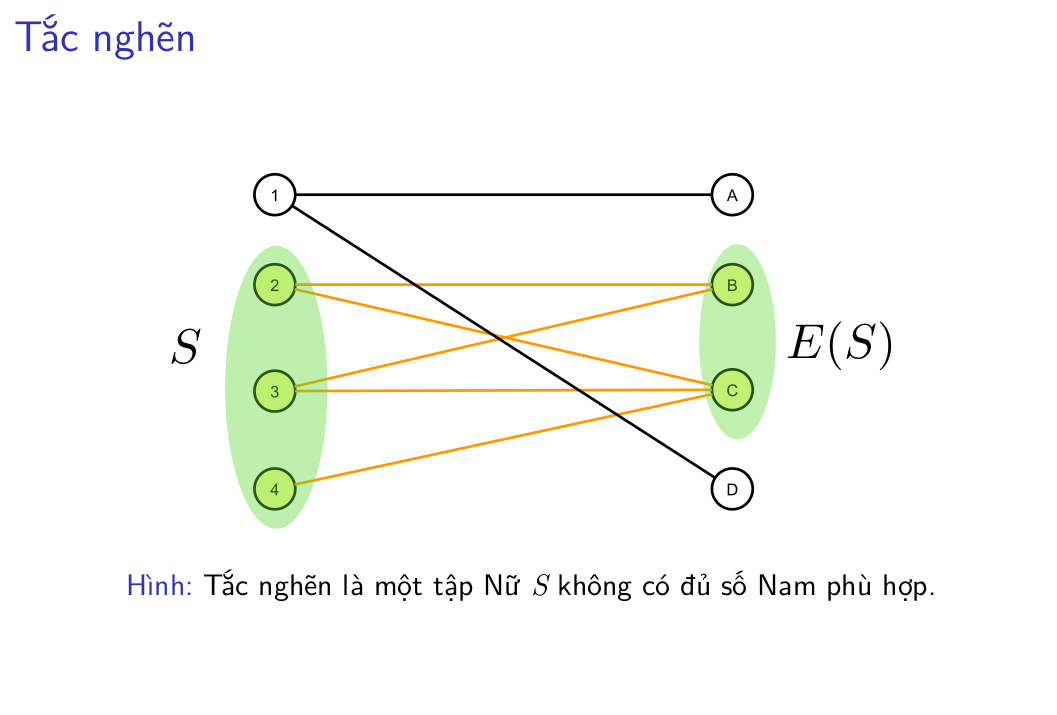
Đọc thêm: Quản lý quan hệ khách hàng (CMR) là gì? CRM tạo thành công cho Marketing ra sao?

3. Điểm danh các lý thuyết mà bạn sẽ được học trong toán rời rạc

Học toán Discrete mathematics, bạn sẽ được học qua ba phần trên và trong 3 chương học, toán rời rạc sẽ dạy cho bạn các lý thuyết như sau:

• Lý thuyết tập hợp: Lý thuyết tập hợp định nghĩa là nghiên cứu về các tập hợp là một tập hợp các đối tượng được sắp xếp trong một nhóm. Tập hợp được biểu thị bằng ký hiệu dấu ngoặc nhọn {}.
• Lý thuyết đồ thị: Nó được nghiên cứu từ đồ thị, biểu đồ là một cấu trúc toán học được sử dụng để ghép nối mối quan hệ các đối tượng. Đồ thị là một trong những đối tượng nghiên cứu chính trong Toán học rời rạc.
• Logic: Logic trong Toán học rời rạc có thể được định nghĩa là nghiên cứu của các suy luận hợp lệ.
• Hoán vị: Đây là cách sắp xếp khác nhau có thể được thực hiện với một số bộ nhất định lấy một số hoặc tất cả trong một trình tự cụ thể tại một thời điểm.
• Kết hợp: Việc lựa chọn một số đối tượng trong bộ môn này lấy một số hoặc tất cả chúng tại một thời điểm được gọi là kết hợp. Thứ tự lựa chọn không quan trọng đối với sự kết hợp trong Discrete mathematics.
• Trình tự: Theo một số quy tắc xác định cụ thể, một tập hợp các số được sắp xếp theo một thứ tự xác định được gọi là Trình tự. Dãy là một hàm có miền là tập hợp tất cả các số tự nhiên có thể đếm được.

4. Phương pháp học toán rời rạc một cách hiệu quả

• Để học được Discrete mathematics một cách hiệu quả, bạn cần sử dụng một số phương pháp học bộ môn này như sau:
• Bạn cần thực hành bài tập của toán rời rạc như một phần quan trọng trong quá trình học tập. Bạn sẽ học được phần lớn càng nhiều càng bài tập càng tốt, bao gồm cả bài tập mỗi phần và các bài tập giảng viên cung cấp.
• Bạn cố gắng tự giải bài tập trước khi xem lời giản, đây là một yêu cầu quan trọng với người học. Bạn chỉ cần đạt được nhiều kiến thức nhất khi trải qua quá trình 10 tự làm tự học.
• Người học không nên bỏ được một buổi học toán rời rạc nào, thời gian học trên lớp là quá trình trao đổi rất tốt giữa giảng viên giữa sinh viên.
• Nếu học viên học ít hơn 3 ngày trong tuần thì học viên đang lãng phí thời gian của mình. Do đó, bạn nên học tập thường xuyên môn này.
• Để học môn này thuận lợi, người học cần tạo cho mình một môi trường thoải mái, có thể đan xen giữa việc giải toán và nghỉ ngơi. Cuối cùng, không bao giờ quên bài giảng mà giảng viên đã dạy bạn.
• Dù bạn có khả năng vượt qua các kỳ thi bằng cách học trước kỳ thi nhưng với cách học như vậy thì kiến thức toán học của bạn chỉ đi vào bộ nhớ tạm thời mà thôi. Kết quả cuối cùng là kiến thức toán của bạn sẽ mức độ không tồn tại lâu dài với cách học sổi. Vì thế, bạn cần phải nghiên cứu thật kỹ để hiểu sâu hơn về bộ môn này.

Đọc thêm: Ngành hóa dược học khối gì? Mức lương, cơ hội việc làm và trường đào tạo

5. Ứng dụng thực tế và một số ví dụ của toán học rời rạc

Ứng dụng của toán học rời rạc

Discrete mathematics là môn học tiên quyết và hiệu quả để người học có thể nâng cao tư duy toán học trong phân tích, thiết kế thuật toán và rèn luyện kỹ năng lập trình với các thuật toán vô cùng phức tạp. Sau đây là những trường hợp sử dụng toán rời rạc, cụ thể:

• Tìm ra password hợp lệ cho một hệ thống máy tính
• Tìm đường nối giữa hai máy tính trong một mạng
• Tìm địa chỉ internet hợp lệ
• Tìm đường đi ngắn nhất giữa hai máy tính trong một mạng
• Tìm ra các bước trong quá trình sắp xếp
• Xây dựng thuật toán cho AI trong game
• Xây dựng trí thông minh cho trí tuệ nhân tạo
• Giả lập các môi trường cả về phần mềm trong lập trình tự động của robot và trong game (như sóng vỗ, lửa cháy,…)
• Đặc biệt sử  dụng toán rời rạc giúp bạn rút gọn code tiết kiệm thời gian lập trình.

Ví dụ về Toán học rời rạc

Ví dụ 1: Xác định xem có bao nhiêu cách chia 3 giải thưởng cho 4 nam sinh khi

i) Không ai được nhiều hơn một giải thưởng.

ii) Một cậu bé có thể nhận được bất kỳ số giải thưởng nào.

Giải pháp:

i) Giải nhất có thể được trao theo 4 cách, trong đó người ta không được nhiều hơn một giải, hai giải còn lại có thể được trao theo 3 cách và 2 giải tương ứng.

Tổng số cách = 4 x 3 x 2 = 24.

ii) Vì không có hạn chế, mỗi giải thưởng có thể được trao theo 4 cách.

Tổng số cách = 4 3 = 64.

Ví dụ 2: Tìm tổng của tất cả các số có bốn chữ số được tạo thành bằng cách sử dụng 2, 3, 6, 9 trong đó không có chữ số nào được lặp lại.

Giải pháp:

Nếu 2 chiếm chỗ của hàng đơn vị thì 3 chữ số còn lại có thể được sắp xếp thành 3! = 6 cách. Tương tự, nếu 2 chiếm vị trí của mười, hàng trăm, hàng nghìn, trong mỗi trường hợp này, chúng ta nhận được 3! những con số. Do đó, giá trị vị trí đóng góp bằng 2 vào tổng khi nó chiếm khác

các giá trị.

(3!) (2) + (3!) (20) + (3!) (200) + (3!) (2000) = 3! (2) (1111)

Tương tự, các giá trị do 3, 6, 9 đóng góp vào tổng là

3! (3) (1111), 3! (6) (1111), 3! (9) (1111) tương ứng.

Tổng yêu cầu là 3! (1111) (2 + 3 + 6 + 9) = 1,33,320

Đọc thêm: Ngôn ngữ lập trình bậc cao là gì? Một số dạng ngôn ngữ lập trình bậc cao nổi trội

Toán rời rạc là môn cơ sở ngành của hầu hết các môn có dính dáng tới máy tính, và nó là một môn cũng rất quan trọng cho các bạn nào theo ngành IT. Toán rời rạc cung cấp cho mọi người những kiến thức cơ bản về tổ hợp và lý thuyết đồ thị.Như vậy, 1900 - tin tức việc làm vừa cung cấp những thông tin hữu ích. Hy vọng qua bài viết bạn hiểu được tầm quan trọng của Toán rời rạc.