Câu hỏi trắc nghiệm CHƯƠNG 5: Đồ thị (có đáp án)
TÓM TẮT NỘI DUNG CƠ BẢN
Xem thêm: Tóm tắt lý thuyết Quan hệ
CÂU HỎI TRẮC NGHIỆM
1. Điều kiện để đồ thị vô hướng với n>2 đỉnh có cây khung là…?
A. Đồ thị có trọng số
B. Đồ thị có chu trình
C. Đồ thị liên thông
D. Đồ thị có đường đi từ đỉnh đầu đến đỉnh x
2. Cho đồ thị G = (V, E), |V| = n, |E| = m. Khi đó đường đi Euler trong G có:
A. n đỉnh
B. m cạnh
C. n - 1 đỉnh
D. m - 1 cạnh
3. Cho G = (V, E) là đồ thị đầy đủ với |V| = 4. Khi đó phát biểu nào sau đây là đúng?
A. G là đồ thị liên thông.
B. G là đơn đồ thị.
C. Tất cả các đỉnh của G đều có bậc 3.
D. G không là đồ thị phẳng
4. Một đơn đồ thị vô hướng liên thông có 9 đỉnh, các đỉnh có bậc lần lượt là 2, 2, 2, 3, 3, 3, 4, 4, 5. Tìm số cạnh của đồ thị?
A. 10
B. 15
C. 12
D. 14
5. Cho đồ thị G có trọng số như hình sau. G là đồ thị có phải đồ thị Euler không? Vì sao?

A. Có vì các đỉnh của đồ thị đều có bậc chẵn
B. Không, vì nó chứa các đỉnh bậc lẻ (a,k,m,c,d,h)
C. Không, vì nó chứa các đỉnh bậc chẵn (a,k,m,c,d,h)
D. Có, vì nó chứa các đỉnh bậc chẵn (a,k,m,c,d,h)
6. Tìm đường đi ngắn nhất từ đỉnh A đến các đỉnh còn lại trong đồ thị sau. Đỉnh E được gán trọng số nhỏ nhất là?
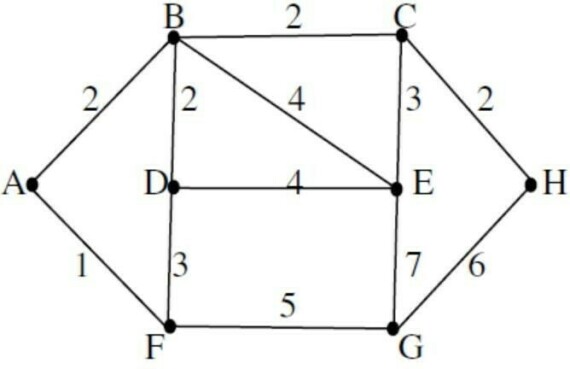
A. 6
B. 7
C. 4
D. 13
7. Chu trình Hamilton là…?
A. Chu trình sơ cấp đi qua tất cả các cạnh của đồ thị
B. Là chu trình đi qua tất cả các cạnh của đồ thị, mỗi cạnh đúng 1 lần
C. Chu trình đơn đi qua tất cả các đỉnh của đồ thị
D. Là chu trình sơ cấp đi qua tất cả các đỉnh của đồ thị, mỗi đỉnh đúng 1 lần
8. Hãy cho biết đồ thị nào sau đây là đồ thị Euler?

A. Đồ thị A
B. Đồ thị B
C. Đồ thị C
D. Đồ thị D
9. Cây là đồ thị vô hướng liên thông…?
A. Không có chu trình Hamilton
B. Không có đỉnh treo
C. Không có chu trình
D. Không có chu trình Euler.
10. Giả sử G=(V,E) là đồ thị vô hướng liên thông có n đỉnh. T là cây khung (cây bao trùm) của đồ thị G. Khẳng định nào sau đây không tương đương với các khẳng định còn lại?
A. T liên thông, không có chu trình
B. T liên thông, có n-1 cạnh
C. T không có chu trình, có n-1 cạnh
D. T liên thông và các đỉnh đều có bậc chẵn
11. Giả sử G=(V,E) là đồ thị vô hướng liên thông có n đỉnh. T=(V,H) được gọi là cây khung (cây bao trùm) của đồ thị G nếu…?
A. T liên thông và mỗi cạnh của nó đều là cầu
B. Nếu thêm vào T 1 cạnh thì T không còn là đồ thị
C. T liên thông, có n-1 cạnh và HÍE
D. T liên thông và có nhiều hơn n-1 cạnh
12. Cây là đồ thị vô hướng liên thông…?
A. Không có đỉnh treo
B. Có 2 đỉnh treo
C. Không có chu trình
D. Đồ thị vô hướng (có hướng) có chu trình không âm
13. Cho đồ thị G như hình vẽ. Tìm cây bao trùm nhỏ nhất theo thuật toán Kruskal?
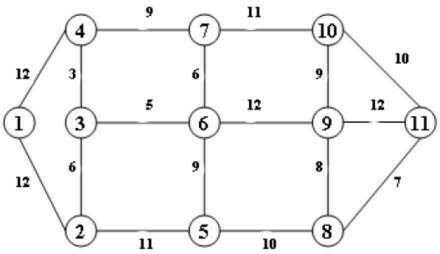
A. T={(3,4),(3,6),(2,3),(3,5),(5,6),(5,8),(8,11),(8,9),(9,10),(1,2)}
B. T={(3,4),(3,6),(2,3),(6,10), (5,6),(5,8), (8,11),(8,9),(9,10),(1,2)}
C. T={(3,4),(3,6),(2,3),(6,7), (5,6),(6,8), (8,11),(8,9),(9,10),(1,2)}
D. T={(3,4),(3,6),(2,3),(6,7), (8,11), (8,9),(5,6),(9,10),(5,8), (1,2)}
14. Điều kiện để đồ thị vô hướng với n>2 đỉnh có cây khung là…?
A. Đồ thị có trọng số
B. Đồ thị có chu trình
C. Đồ thị liên thông
D. Đồ thị có đường đi từ đỉnh đầu đến đỉnh x
15. Cho đồ thị như hình vẽ. Thuật toán Dijkstra tìm đường đi ngắn nhất từ đỉnh 1 đến các đỉnh còn lại, nhãn cực tiểu của đỉnh 5 là bao nhiêu?

A. 14
B. 11
C. 6
D. 13
16. Cho đồ thị như hình vẽ. Đường đi ngắn nhất từ đỉnh 1 đến đỉnh 9 là…?

A. 1→2→6→8→9
B. 1→2→5→7→9
C. 1→3→5→8→9
D. 1→4→6→8→9
17. Thuật toán Dijkstra áp dụng cho?
A. Đồ thị vô hướng có trọng số
B. Đồ thị có hướng có trọng số
C. Đồ thị vô hướng, có hướng có trọng số không âm
D. Đồ thị vô hướng, có hướng có chu trình và trọng số không âm
18. Thuật toán Dijkstra được dùng để?
A. Tìm đường đi ngắn nhất giữa 2 đỉnh của đồ thị
B. Tìm đường đi ngắn nhất giữa các cặp đỉnh của đồ thị
C. Tìm đường đi ngắn nhất giữa 2 đỉnh bất kì của đồ thị
D. Tìm đường đi ngắn nhất từ 1 đỉnh đến các đỉnh còn lại của đồ thị
19. Thuật toán Prim dùng để…?
A. Tìm chu trình ngắn nhất trên đồ thị
B. Tìm đường đi ngắn nhất trên đồ thị
C. Tìm cây khung của đồ thị
D. Tìm cây khung nhỏ nhất của đồ thị
20. Có thể xây dựng cây khung của đồ thị (không trọng số) bằng thuật toán….?
A. BFS,DFS
B. Prim
C. Kruskal
D. Dijkstra
21. Phát biểu nào sau đây là đúng:
A. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
B. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
C. Đồ thị G là đơn đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
D. Đồ thị G là đơn đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
22. Phát biểu nào sau đây là đúng:
A. Đồ thị G là đa đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
B. Đồ thị G là đa đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
C. Đồ thị G là đa đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
D. Đồ thị G là đa đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh
23. Phát biểu nào sau đây là đúng:
A. Đồ thị G là giả đồ thị khi và chỉ khi G không có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
B. Đồ thị G là giả đồ thị khi và chỉ khi G có khuyên và bất kỳ hai đỉnh phân biệt nào cũng được nối với nhau bởi không quá một cạnh.
C. Đồ thị G là giả đồ thị khi và chỉ khi G không có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh.
D. Đồ thị G là giả đồ thị khi và chỉ khi G có khuyên và trong G có tồn tại một cặp đỉnh phân biệt được nối với nhau bởi nhiều hơn một cạnh
24. Cho G là đồ thị có hướng, phát biểu nào sau đây là chính xác nhất:
A. G là đơn đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung (cùng chiều) nối với nhau và có thể có khuyên.
B. G là đơn đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung nối với nhau và không có khuyên.
C. G là đơn đồ thị có hướng khi và chỉ khi trong G có một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và không có khuyên.
D. G là đơn đồ thị có hướng khi và chỉ khi trong G có một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và có thể có khuyên
25. Cho G là đồ thị có hướng, phát biểu nào sau đây là chính xác nhất:
A. G là đa đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung (cùng chiều) nối với nhau và có thể có khuyên.
B. G là đa đồ thị có hướng khi và chỉ khi trong G đối với mỗi cặp đỉnh khác nhau có không quá một cung nối với nhau và không có khuyên.
C. G là đa đồ thị có hướng khi và chỉ khi trong G có tồn tại một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và không có khuyên.
D. G là đa đồ thị có hướng khi và chỉ khi trong G có tồn tại một cặp đỉnh khác nhau được nối với nhau bởi nhiều hơn một cung (cùng chiều) và có thể có khuyên
26. Giả sử G=(V,E) là đồ thị vô hướng. Đỉnh x gọi là đỉnh cô lập nếu:
A. x có bậc 0
B. x có bậc 1
C. x có bậc lẻ
D. x có bậc chẵn
27. Cho đồ thị G = (V, E), |V| = n đỉnh, |E| = m cạnh. Khi đó đường đi Hamilton trong G có:
A. n đỉnh
B. m cạnh
C. n - 1 đỉnh
D. m - 1 cạnh
28. Phát biểu nào sau đây là chính xác nhất:
A. Cho G là đồ thị bất kỳ. Một đường đơn trong G là đường Euler khi và chỉ khi đường đơn đó đi qua tất cả các cạnh trong G và mỗi cạnh xuất hiện đúng một lần.
B. Cho G là đồ thị bất kỳ. Một đường đơn trong G là đường Euler khi và chỉ khi đường đơn đó đi qua tất cả các đỉnh trong G và mỗi đỉnh xuất hiện đúng một lần.
C. Cho G là đồ thị bất kỳ. Một đường đi trong G là đường Euler khi và chỉ khi đường đơn đó đi qua các cạnh trong G.
D. Cho G là đồ thị bất kỳ. Một đường đơn trong G là đường Euler khi và chỉ khi đường đơn đó đi qua tất cả các đỉnh trong G.
29. Phát biểu nào sau đây là chính xác nhất:
A. Cho G là đồ thị bất kỳ. Một đường đi trong G là đường Hamilton khi và chỉ khi đường đi đó đi qua tất cả các cạnh trong G và mỗi cạnh xuất hiện đúng một lần.
B. Cho G là đồ thị bất kỳ. Một đường sơ cấp trong G là đường Hamilton khi và chỉ khi đường đi đó đi qua tất cả các đỉnh trong G và mỗi đỉnh xuất hiện đúng một lần.
C. Cho G là đồ thị bất kỳ. Một đường sơ cấp trong G là đường Hamilton khi và chỉ khi đường đi đó đi qua tất cả các cạnh trong G.
D. Cho G là đồ thị bất kỳ. Một đường đi trong G là đường Hamilton khi và chỉ khi đường đi đó đi qua tất cả các đỉnh trong G.
30. Phát biểu nào sau đây là chính xác nhất. Cho đồ thị G =. Chu trinh đơn trong G là:
A. Chu trình mà trong chu trình đó mỗi cạnh xuất hiện đúng một lần.
B. Chu trình mà trong chu trình đó mỗi đỉnh xuất hiện đúng một lần.
C. Chu trình đi qua tất cả các cạnh của G.
D. Chu trình đi qua tất cả các đỉnh của G.
31. Phát biểu nào sau đây là chính xác nhất. Cho đồ thị G =. Chu trinh sơ cấp trong G là:
A. Chu trình mà trong chu trình đó mỗi cạnh xuất hiện đúng một lần.
B. Chu trình mà trong chu trình đó mỗi đỉnh xuất hiện đúng một lần.
C. Chu trình đi qua tất cả các cạnh của G.
D. Chu trình đi qua tất cả các đỉnh của G.
32. Cho đồ thị G bất kỳ, số đỉnh bậc lẻ trong G luôn luôn là một số:
A. Số chẵn
B. Số lẻ
C. Có thể chẵn, có thể lẻ
33. Cho G= là đồ thị bất kỳ. Bậc của đồ thị G bằng …
A. Hai lần số cạnh
B. Số cạnh
C. Số đỉnh
D. Hai lần số đỉnh
34. Cho đồ thị G có bậc là 10. Số cạnh của đồ thị G là:
A. 4
B. 5
C. 6
D. 7
35. Cho đồ thị G có 5 đỉnh có bậc lần lượt là 2, 2, 3, 4, 5. Bậc của đồ thị G là:
A. 8
B. 16
C. 10
D. 20
36. Cho đồ thị vô hướng cạnh có trọng số như hình vẽ. Cây khung nhỏ nhất có tổng trọng số là:

A. 18
B. 10
C. 7
D. 24
ĐÁP ÁN
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| C |
B |
C |
D |
B |
A |
D |
A |
C |
D |
| 11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| C |
C |
D |
C |
B |
C |
C |
D |
D |
A |
| 21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
| A |
C |
D |
A |
D |
A |
A |
A |
B |
A |
| 31 |
32 |
33 |
34 |
35 |
36 |
|
|
|
|
| B |
A |
A |
B |
B |
B |
|
|
|
|
Xem thêm:
Xem thêm câu hỏi trắc nghiệm Toán rời rạc
Câu hỏi trắc nghiệm Toán rời rạc: Tập hợp, hàm
Câu hỏi trắc nghiệm Toán rời rạc: Các phép đếm
Câu hỏi trắc nghiệm Toán rời rạc: Quan hệ
Câu hỏi trắc nghiệm Toán rời rạc: Logic mệnh đề
Việc làm dành cho sinh viên:
Việc làm thực tập sinh kiểm toán
Việc làm gia sư các môn cập nhật theo ngày mới nhất
Việc làm thêm nhân viên phục vụ nhà hàng/ quán cafe dành cho sinh viên
Việc làm cộng tác viên kế toán
Mức lương của Thực tập sinh kế toán là bao nhiêu?










