ĐẠI SỐ BOOL VÀ HÀM BOOL
ĐẠI SỐ BOOL
Định nghĩa 4.1.1:
Một đại số Bool là tập hợp ? cùng với hai phép tính (hai ngôi) ? và ? thỏa mãn các tính chất sau
1. Tính kết hợp : với mọi ?, ?, ? ∈ ?:
? ? ( ? ? ?) = ( ? ? ?) ? ?
và ? ? ( ? ? ?) = ( ? ? ?) ? ?
2. Tính giao hoán: với mọi ?, ?, ? ∈ ?:
? ? ? = ? ? ?
và ? ? ? = ? ? ?
3. Tính phân bố: với mọi ?, ?, ? ∈ ?:
? ? ( ? ? ?) = ( ? ? ?) ? ( ? ? ?)
và ? ? ( ? ? ?) = ( ? ? ?) ? ( ? ? ?)
4. Phần tử trung hòa:
Tồn tại hai phần tử trung hòa 0,1 đối với hai phép toán ?,? sao cho với mọi ? ∈ ? ta có:
? ? 0 = ?
và ? ? 1 = ?
5. Phần tử bù: với mọi ? ∈ ?, tồn tại ∈ ? sao cho:
? ? ?̅ = 1
và ? ? ?̅ = 0
Ví dụ:
1. Một dàn bù phân bố là một đại số Bool với hai phép tính ?,? chính là sup và inf của hai phần tử. Đặc ?( ?) là một đại số Bool dối với các phép tính tập hợp ? và ∩. Cũng thế ? cũng là một đại số Bool đối với các phép nối rời ? và nối liền ? của hai dạng mệnh đề. Do 30 không chia hết cho chính phương, ࣯30 là dàn bù phân bố và do đó là một đại số Bool đối với các phép toán :
? ? ? = ?????( ?, ?)
và ? ? ? = ?????( ?, ?)
2. Tập hợp ? = { 0,1} là một đại số Bool dối với các phép toán :
? ? ? = ??
? ? ? = ? + ? − ??
Phần bù của ? chính là ?̅ = 1 − ?
Đại số Bool này đóng vai trò quan trọng trong lý thuyết về các hàm Bool.
Chú ý: phần bù ?̅ của phần tử ? là duy nhất và hơn nữa ta có qui tắc De Morgan (Bài tập).
= ?̅ ? ?̅ và = ?̅ ? ?̅
Trong các ví dụ trên, các phép toán đại số Bool được định nghĩa còn tự nhiên hơn cấu trúc thứ tự của dàn bù phân bố. vấn đề được đặt ra là liệu có thể suy cấu trúc của dàn bù phân bố từ cấu trúc đại số Bool không? Định lý sau đây là câu trả lời:
Định nghĩa 4.1.1: trong đại số Bool ?, định nghĩa quan hệ:
? ≺ ? ⟺ ? ? ? = ?
Khi ấy ≺ là một thứ tự trên sao cho ? là một dàn bù phân bố đối với thứ tự này.
Hơn nữa, với ?, ? ∈ ? ta có:
sup( ?, ?) = ? ? ?
inf( ?, ?) = ? ? ?
Chứng minh: Trước hết ta kiểm tra ≺ là một thứ thự trên ?. Với mọi ? ∈ ? ta có:
? ? ? = ( ? ? ?) ? 0
= ( ? ? ?) ? ( ? ? ?̅)
= ? ? ( ? ? ?̅)
= ? ? 1 = ? (4.1.1)
nghĩa là ? ≺ ?
Mặt khác với ?, ? ∈ ? sao cho ? ≺ ? và ? ≺ ? ta có:
? ? ? = ? ?à ? ? ? = ?
Do tính giao hoán của ? ta có ? = ?
Với ?, ?, ? ∈ ? sao cho ? ≺ ? và ? ≺ ? ta có:
? ? ? = ? ?à ? ? ? = ?
Suy ra
? ? ? = ( ? ? ?) ? ? = ? ? ( ? ? ?)
= ? ? ? = ?
Nghĩa là ? ≺ ?
Tóm lại ≺ là một thứ tự trên ?.
Với ?, ? ∈ ? tùy ý, ta có
( ? ? ?) ? ? = ( ? ? ?) ? ?
Nhưng ? ? ? = ? ( do 4.1.1)
Nên ( ? ? ?) ? ? = ? ? ?
Nghĩa là ? ? ? ≺ ?
Tương tự ? ? ? = ? ? ? ≺ ?
Như thế ? ? ? là chặn dưới chung của ?, ?
Gọi ? là một chặn dưới chung bất kỳ của ?, ?. Ta có:
? ? ? = ? ?à ? ? ? = ?
Do đó ? ? ( ? ? ?) = ( ? ? ?) ? ? = ? ? ? = ?
nghĩa là ? ≺ ? ? ?
Như thế ? ? ? = inf( ?, ?)
Bây giờ do iv) của Định nghĩa 4.1.1, 1 chính là phần tử lớn nhất. Mặt khác, với ? ∈ ?
0 ? ? = ( 0 ? ?) ? 0
= ( 0 ? ?) ? ( ? ? ?̅)
= ( 0 ? ?̅) ? ?
= ?̅ ? ? = 0 (4.1.1)
Nghĩa là 0 là phần tử bé nhất của ?.
Sau cùng với mọi ?, ? ∈ ?, ta có:
? ? ( ? ? ?) = ( ? ? 0) ? ( ? ? ?)
∅ = ? ? ( 0 ? ?)
Mà 0 ? ? = 0 ( do 4.1.2)
Nên ? ? ( ? ? ?) = ? ? 0 = ?
Nghĩa là ? ≺ ? ? ?
Tương tự ? ≺ ? ? ? = ? ? ?
Gọi ? là mộ chặn trên chung của ?, ? ta có:
( ? ? ?) ? ? = ( ? ? ?) ? ( ? ? ?)
= ? ? ?
Nghĩa là ? ? ? ≺ ?
Như thế ? ? ? = sup( ?, ?)
Tóm lại ? là một dàn phân bố với phần tử lớn nhất và bé nhất là 1,0. Hơn nữa, do v) của Định lý 4.1.1 ?̅ chính là phần bù của ?. đpcm
Do Định lý 4.1.1, mỗi đại số Bool hữu hạn được liên kết với một biểu đồ Hasse. Ta hãy quan sát aho đại số Bool ࣯30 và ?({ ?, ?, ?}) . Tuy được định nghĩa khác nhau, các đại số Bool này có hai biểu đồ Hasse “đồng dạng”
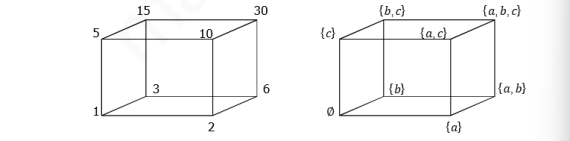
Từ hai biểu đồ trên ta có thể xây dựng một song ánh ? giữa và ?({ ?, ?, ?}) sao cho các đỉnh tương ứng với nhau 1 ⟼ ∅, 2 ⟼ { ?}, 3 ⟼ { ?},… và hai đỉnh được nối bởi một cạnh của ࣯30 sẽ tương ứng với hai đỉnh được nối bởi một cạnh của ?({ ?, ?, ?}) . Nói cách khác ta có một đẳng cấu giữa các tập hợp có thứ tự. Do Định lý 3.4.1 sup và inf của hai phần tử ?, ? trong ࣯30 tương ứng với sup, inf của ?( ?) , ?( ?). Nói cách khác ? là một đẳng cấu giữa các đại số Bool theo định nghĩa sau:
Định nghĩa 4.1.2:
Một đẳng cấu giữa hai đại số Bool ? và ? là một song ánh ?: ? ⟷ ? sao cho với mọi ?, ? ∈ ? ta có:
?( ? ? ?) = ?( ?) ? ?( ?)
và ?( ? ? ?) = ?( ?) ? ?( ?)
Mệnh đề 4.1.2 :
Nếu ?: ? ⟷ ? là một đẳng cấu Đại số Bool thì ? cũng là đẳng cấu tập hợp có thứ tự với thứ tự trên ? và ? xác định bởi Định lý 4.1.1. Đặc biệt nếu 0,1 là phần tử trung hòa của ?,? trong ? thì ?( 0), ?( 1) là phần tử trung hòa của ?,? trong ?.
Chứng minh: giả sử ?, ? là hai phần tử trong ? sao cho ? ≺ ?. Khi ấy ta có:
? ? ? = ? ⟹ ?( ?) ? ?( ?) = ?( ?)
⟹ ?( ?) ≺ ?( ?)
Do 0 và 1 cũng là phần tử bé nhất và lớn nhất của ?, ta thấy ?( 0) và ?( 1) cũng là phần tử bé nhất và lớn nhất của ?, nghĩa là phần tử trung hòa đối với các phép toán ?,? trong ? l đpcm
Trở lại hai đại số Bool ࣯30 và ?({ ?, ?, ?}) . Sự đẳng cấu của chúng không phải là trường hợp cá biệt. Ta có:
Đinh lý 4.1.3 (Stone): một đại số Bool hữu hạn ? luôn lương đẳng cấu với ?( ?), trong đó ? là một tập hợp hữu hạn.
Hệ quả 1: Số phần tử của một đại số Bool hữu hạn là một ũy thừa của 2.
Hệ quả 2: Hai đại số Bool hữu hạn có cùng số phần tử thì đẳng cấu với nhau.
Chứng minh: Thật vậy hai đại số Bool cho trước sẽ đẳng cấu với như sau:
?: ?( ?1) → ?( ?2)
? ⟼ ƒ( ?)
Khi ấy ta có:
ƒ( ? ? ?) = ƒ( ?) ? ƒ( ?)
nghĩa là
?( ? ? ?) = ?( ?) ? ?( ?)
Hơn nữa do ƒ là song ánh ta cũng có:
ƒ( ? ∩ ?) = ƒ( ?) ∩ ƒ( ?)
Nghĩa là
?( ? ? ?) = ?( ?) ? ?( ?)
Bây giờ để chứng minh Định lý Stone ta cần tìm tập hợp ?. Để ý rằng ta có một đơn
ƒ: ? → ?( ?)
? ⟼ { ?}
Hơn nữa trong ?( ?) các tập hợp { ?} chính là các trội trực tiếp của ∅. Từ đó ta có:
Định nghĩa 4.1.3
Trong một đại số Bool ?, một trội trực tiếp của phần tử bé nhất được sọi là một nguyên tử của ?.
Bổ đề 4.1.4:
Giả sử ? là một đại số Bool hữu hạn với phần tử bé nhất 0. Khi ấy mọi phần tử ? ≠ 0 đều có thể viết dưới dạng: ? = ?1 ? ?2 ? …? ??
trong đó { ?1, ?2,…, ??} là tập hợp các nguyên tử trội bởi ?. Hơn nữa nếu ?1, ?2,…, ?? là các nguyên tử sao cho:
? = ?1 ? ?2 ? …? ?? thì { ?1, ?2,…, ??} = { ?1, ?2,…, ??}
Chứng minh: Trước hết ?\ { 0} là một tập hợp sắp thứ tự hữu hạn chứa ?( ≠ 0) nên tồn tại một phần tử tối tiểu ? ≺ ?. Rõ ràng ? là một nguyên tử của ?. Nói cách khác tập hợp { ?1, ?2,…, ??} các nguyen tử trội bởi ? là không ∅.
Đặt ? = ?1 ? ?2 ? …? ??
Rõ ràng ? ≺ ?.
Ta có:
? = ? ? ( ? ? ?̅) = ( ? ? ?) ? ( ? ? ?̅)
= ? ? ( ? ? ?̅)
Giả sử ( ? ? ?̅) ≠ 0
Khi ấy theo trên tồn tại một nguyên tử ? ≺ ? ? ?̅. Như thế ? = ?i với 1 ≤ i ≤ ? nào đó
Đặt ? = ?1 ? ?2 ? …? ?i−1 ? ?i−1 ? …? ??
Ta có ? = ? ? ?
Do đó ?̅ = ?̅ ? ?̅
Suy ra ? = ? ? ?̅ = ? ? ?̅ ? ?̅ = 0: mâu thuẫn.
Như thế ( ? ? ?̅) = 0
Nghĩa là ? = ?
Sau cùng giả sử ?1, ?2,…, ?? là các nguyên tử trội bởi ? sao cho
? = ?1 ? ?2 ? …? ??
Ta có :
{ ?1, ?2,…, ??} ⊂ { ?1, ?2,…, ??}
Mặt khác, với mỗi j cố định, 1 ≤ i ≤ ? ta có:
?j = ?j ? ? = (?j ? ?1) ? (?j ? ?2) ? …(?j ? ??)
Suy ra tồn tại ? sao cho 1 ≤ ? ≤ ? và
0 ≠ ?j ? ?k ≺ ?j
Do ?j là nguyên tử ta có: ?j ? ?k = ?j
Nghĩa là ?j ≺ ?k
Do ?k là nguyên tử và ?j ≠ 0 ta có ?j = ?k
Như thế
{ ?1, ?2,…, ??} ⊂ {?1, ?2,…, ??}
Nghĩa là
{ ?1, ?2,…, ??} = { ?1, ?2,…, ??} l đpcm
Gọi ? là tập hợp tất cả các nguyên tử của ?. Nhờ Bổ đề 4.1.4, ta có một ánh xạ ?: ? → ?( ?) được định nghĩa như sau:
- ?( 0) = ∅
- Nếu ? ≠ 0 thì ?( ?) là tập hợp tất cả các nguyên tử trội bởi ?. Bây giờ Định lý 4.1.3 là hệ quả của
Định lý 4.1.5 : ? là một đẳng cấu giữa ? và ?( ?) .
Chứng minh: Giả sử 0 ≠ ? ≺ ?. Khi ấy các nguyên tử trội bởi ? cũng là nguyên tử trội bởi ? nên ?( ?) ⊂ ?( ?)
Ngược lại giả sử 0 ≠ ?( ?) ⊂ ?( ?)
Ta viết ?( ?) = {?1, ?2,…, ??} và ?( ?) = { ?1, ?2,…, ??} Do Bổ đề 4.1.4 ta có:
? = ?1 ? ?2 ? …? ??
và ? = ?1 ? ?2 ? …? ??
Do { ?1, ?2,…, ??} ⊂ { ?1, ?2,…, ??} nên ? ≺ ?
Trường hợp ? = 0 là hiển nhiên.
Tóm lại, ta đã chứng minh: ( ? ≺ ?) ⟺ (?( ?) ⊂ ?( ?) )
Đặc biệt nếu ?( ?) = ?( ?) thì ? ≺ ? và ? ≺ ? nên ? = ?: ? là đơn ánh.
Sau cùng, giả sử { ?1, ?2,…, ??} ⊂ ?
Đặt ? = ?1 ? ?2 ? …? ?? và ?( ?) = { ?1, ?2,…, ??} Do Bổ đề 4.1.4
? = ?1 ? ?2 ? …? ??
và { ?1, ?2,…, ??} = { ?1, ?2,…, ??}.
Như thế ? là toàn ánh. l đpcm
HÀM BOOL
Xét sơ đồ mạch điện gồm 3 ngắt điện:

Tùy theo các ngắt điện ?, ?, ? được đóng hay mở sẽ có dòng điện đi từ ? đến ? hay không. Để biết các ngắt điện điều khiển việc cho dòng điện đi qua hay không, ta vẽ ra sơ đồ cho tất cả mọi trường hợp. Tuy nhiên điều này không thực hiện được nếu số ngắt điện quá lớn. Ví dụ nếu có 100 ngắt điện sẽ có 2100 sơ đồ khác nhau. Ngay cả trong trường hợp số ngắt điện bé, thì vẫn cần một cách sắp xếp có hệ thống các sơ đồ để có thể tra cứu dễ dàng từng trường hợp.
Chẳng hạn ta có thể liên kết với mỗi ngắt điện một biến lấy giá trị 1 nếu ngắt điện đóng và 0 nếu ngắt điện mở. Trong ví dụ về mạch điệm nói trên ta có ba biến ?, ?, ?. Ngoài ra toàn mạch điện cò được liên kết với biến ? lấy giá trị 1 nếu có dòng diện đi từ ? đến ? và lấy giá trị 0 trong trường hợp không có dòng diện nào đi từ ? đến ?. với tương ứng như vậy ta có thể liệt kê tất cả các trường hợp trong bảng giá trị như sau:
|
?
|
?
|
?
|
?
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
|
0
|
1
|
0
|
0
|
|
0
|
1
|
1
|
1
|
|
1
|
0
|
0
|
1
|
|
1
|
0
|
1
|
1
|
|
1
|
1
|
0
|
1
|
|
1
|
1
|
1
|
1
|
Trong trường ngắt điện lớn thì việc lập bảng giá trị là không thực tế. Ta cần tìm một công thức cho phép biểu diễn hàm ?( ?, ?, ?) theo các biến ?, ?, ? như các hàm đa thức trong trường hợp hàm biến thực chẳng hạn. Mặt khác ta cũng nhận xét rằng bảng trên rất giống bảng chân trị của các dạng mệnh đề. Thật ra khi khảo sát các dạng mệnh đề, điều ta quan tâm không phải là mệnh đề thu được ?( ?, ?, ?,…) khi ta thay các biến mệnh đề ?, ?, ?,… lần lượt bởi các mệnh đề ?, ?, ?,… mà là sự phụ thuộc chân trị của mệnh đề ?( ?, ?, ?,…) vào chân trị các mệnh đề ?, ?, ?,… Nói cách khác ta đồng nhất dạng mệnh đề ?( ?, ?, ?,…) với bảng chân trị của nó. Thực chất ở đây là ta đang xem xét hàm ?( ?, ?, ?,…) theo các biến ?, ?, ?,… trong đó ?, ?, ?,… và cả ?( ?, ?, ?, …) cũng chỉ lấy hai giá trị 0,1. Đó là các hàm Bool theo định nghĩa dưới đây:
Định nghĩa 4.2.1:
Một hàm Bool ? biến là một ánh xạ ?? → ?, trong đó ? = {0,1}. Tập hợp các hàm Bool ? biến được ký hiệu bởi ℱ?.
Chú ý:
1. Các hàm Bool còn được gọi là hàm logic hay hàm nhị phân
2. Nhắc lại tập hợp ? là đại số Bool đối với các phép toán
? ? ? = ??
? ? ? = ? + ? − ??
?̅ = 1 − ?
3. Các biến xuất hiện trong hàm Bool được gọi là biến Bool. Mỗi hàm Bool được liên kết với một bảng tương tự như bảng trên cho biết sự phụ thuộc của hàm Bool theo giá trị các biến Bool. Ta cũng gọi bảng giá trị này là Bảng chân trị của hàm Bool.
4. Theo ký hiệu của Chương 3 ℱ? chính là tập hợp 2? . Do đó số hàm Bool khác nhau chính là |ℱ?| = 2|?? | = 2( 2?)
Mặt khác trong §1, tương ứng ? ⟼ 3Æ là một đẳng cấu của tập hợp có thứ tự ?( ??) và ℱ? trong đó thứ tự trên ℱ? được xác định như sau: với ƒ, ? ∈ ℱ? thì
ƒ ≺ ? ⟺ ∀? = ( ?1, ?2,…, ??) ∈ ??, ƒ( ?) ≤ ?( ?)
Khi ấy sup và inf của hai hàm ƒ, ? được cho bởi:
( ƒ ? ?) ( ?) = ƒ( ?) ? ?( ?)
= ƒ( ?) + ?( ?) − ƒ( ?) ?( ?) , ∀? ∈ ??
và ( ƒ ? ?) ( ?) = ƒ( ?) ? ?( ?)
= ƒ( ?) ?( ?), ∀? ∈ ??
Và phần bù ƒ̅ của hàm Bool ƒ được cho bởi
ƒ̅( ?) = ̅ƒ̅(̅?̅)
= 1 − ƒ( ?) , ∀? ∈ ??
Ta sử dụng ký hiệu thông thường ƒ? và 1 − ƒ để chỉ các hàm ƒ ? ? và ƒ̅ trong đó 1 chỉ hàm hằng ?? → {1}
Với các phép toán trên, ℱ? trở thành một đại số Bool đẳng cấu với ?( ??) . Đặc biệt các nguyên tử trong ℱ? sẽ tương ứng với các nguyên tử trong ?( ??) . mà trong ?( ??) các nguyên tử chính là các tập hợp thu về một điểm nên ta có:
Mệnh đề 4.2.1
Các nguyên tử trong ℱ? là các hàm Bool chỉ khác 0 tại điểm duy nhất, hay nói cách khác, bảng chân trị của nó chỉ có một dòng duy nhất ở đó hàm khác 0. Các này dược gọi là các từ tối tiểu của ℱ?.
Do Định lý Stone ta có:
Định lý 4.2.2 :
Mỗi hàm Bool ƒ đều được viết dưới dạng:
ƒ = ?1 ? ?2 ? …? ?? ( 4.2.1)
Trong đó ?1, ?2,…, ?? là các từ tối tiểu trội bởi ƒ.
Do từ tối tiểu ?i chỉ khác 0 ở duy nhất một dòng, ?i sẽ được trội bởi ƒ khi và chỉ khi dòng mà ?i khác 0 cũng là một trong những dòng mà ƒ khác 0. Từ đó ta có qui tắc viết ra công thức (4.2.1) bằng cách chọn ?i chính là các từ tối tiểu tương ứng với một dòng khác 0 nào đó của ƒ . Chẳng hạn như trong ví dụ về hàm ?( ?, ?, ?) biểu diễn mạch điện ở trên ta có
|
?
|
?
|
?
|
?
|
?1
|
?2
|
?3
|
?4
|
?5
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
0
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
0
|
0
|
|
1
|
0
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
|
1
|
1
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
|
1
|
1
|
1
|
1
|
0
|
0
|
0
|
0
|
1
|
Ta có
? = ?1 ? ?2 ? ?3 ? ?4 ? ?5 (4.2.2)
Bây giờ để có một công thức tường minh cho một hàm Bool bất kỳ, do (4.2.1) ta cần tìm một công thức tường minh cho tất cả các từ tối tiểu. Nhắc lại phép chiếu thứ i được cho bởi:
?i: ?? → ?
( ?1, ?2,…, ??) ⟼ ?i
Rõ ràng bản thân ?i là một hàm Bool ? biến mà giá trị của nó chỉ phụ thuộc vào biến thứ i. Tương tự như trường hợp các hàm thực, ta sẽ dùng cùng ký hiệu ?i dể chỉ hàm Bool
?i: ?i( ?1, ?2,…, ??) = ?i
Với ký hiệu này thì phần bù ?̅i = 1 − ?i cũng là một hàm Bool mà giá trị chỉ phụ thuộc vào biến thứ i. Ta nói ?i, ?̅i là các từ đơn. Có tất cả 2? từ đơn.
Mệnh đề 4.2.3
Các từ tối tiểu đều có thể viết dưới dạng: ? = ?1?2 …?? trong đó ?i = ?i hay ?i = ?̅i
Chứng minh: giả sử ?i là từ đơn bằng ?i hay ?̅i. Ta sẽ chứng minh ? = ?1?2 …?? là một từ tối tiểu. Chính xác hơn gọi ? = ( ?1, ?2,…, ??) là các phần tử của ?? sao cho ?i = 1 nếu ?i = ?i và ?i = 0 nếu ?i = ?̅i. Ta sẽ chứng minh rằng ? khác 0 duy nhất tại ?.
Thật vậy với 1 ≤ i ≤ ? ta có:
?i( ?) = ?i( ?) = ?i = 1
nếu
?i = ?i và ?i( ?) = ?̅i( ?) = ?̅i = 1 nếu ?i = ?̅i
Như thế ?i( ?) = 1 với 1 ≤ i ≤ ?
Suy ra ?( ?) = 1
Mặt khác nếu ? = ( ?1, ?2,…, ??) ≠ ? thì tồn tại i sao cho 1 ≤ i ≤ ? và ?i ≠ ?i.
Khi ấy:
?i( ?) = ?i( ?) = ?i = 0 (vì ? ≠ ?i) nếu ?i = ?i
và ?i( ?) = ?̅i( ?) = ?̅i = ? (vì ? = ?i) nếu ?i = ?̅i
Như thế ?i( ?) = 0 và do đó ?( ?) = 0
Tóm lại ? là từ tối tiểu tương ứng với điểm ?.
Ngược lại giả sử ? là từ tới tiểu khác 0 duy nhất tại điểm ? = ( ?1, ?2,…, ??) . Đặt:
?i = ?i nếu ?i = 1
và ?i = ?̅i nếu ?i = 0
Khi ấy theo chứng minh trên, ?1?2 …?? là từ tối tiểu tương ứng với điểm ? = ( ?1, ?2,…, ??) sao cho:
?i = 1 nếu ?i = ?i
và ?i = 0 nếu ?i = ?̅i
nói cách khác ?i = ?i, 1 ≤ i ≤ ?
Do đó ? = ?1?2 …?? l đpcm
Chú ý:
1. Do mỗi ?i có thể lấy hai giá trị ?i, ?̅i nên ta tìm lại được số từ tối tiểu chính là số phần tử của ?? ∶ 2?.
2. Ta có qui tắc để viết biểu thức của một từ tối tiểu ứng với điểm ? = ( ?1, ?2,…, ??) : viết tích của tất cả các biến ?1?2 …??, sau đó biến thứ i mà ?i = 0 sẽ được gạch đầu. Chẳng hạn trong ví dụ về mạch điện ở trên các từ tối tiểu ?1, ?2,…, ?5 có biểu diễn như sau:
?1 = ?̅??
?2 = ???
?3 = ??̅?
?4 = ???
?5 = ???
Do đó (4.2.2) trở thành: ? = ?̅?? ? ???̅ ? ??̅? ? ???̅ ? ???
Ở đây ta sử dụng quy ước về thứ tự ưu tiên của phép tính nhân dối với phép toán ?: công thức ?? ? ? có nghĩa là phép toán ?? được thực hiên trước rồi mớit hực hiện phép toán
? giữa ?? và ?. Nói cách khác ?? ? ? = ( ??) ? ?
Ngược lại nếu thực hiên phép ? trước ta phải viết: ?( ? ? ?)
3. Tổng quát hơn, do (4.2.1) và Mệnh đề 4.2.3 một hàm Bool bất kỳ ƒ có thể viết như là tổng Bool của các từ tối tiểu trội bởi ƒ, và mỗi từ tối tiểu này được viết như là tích của đủ ? biến. Công thức này được gọi là dạng nối rời chính tắc của ƒ.
4. Thay vì các từ tối tiểu, ta có thể xét các từ tối đại: đó là phần bù của các từ tối tiểu. Khi ấy do Mệnh đề 4.2.3, mỗi từ tối đại sẽ là tổng Bool của ? từ đơn. Hơn nữa áp dụng (4.2.1) cho ƒ̅, ta có thể viết ƒ như là tích của các từ tối đại: đây chính là dạng nối liền chính tắc của hàm Bool ƒ. Từ đây ta chỉ để ý đến dạng nối rời chính tắc và tổng quát hơn các công thức đa thức theo nghĩa dưới đây:
Định nghĩa 4.2.1
i. Một đơn thức là một tích khác 0 của các từ đơn
ii. Một công thức đa thức của hàm Bool ƒ là công thức biểu diễn ƒ dưới dạng tổng Bool của các đơn thức.
Chú ý: Do ?i?i = ?i và ?i?̅i = 0 nên trong một đơn thức ?, biến ?i và ?̅i có thể xuất hiện
nhưng không đồng thời xuất hiện. Nói cách khác mỗi đơn thức có thể viết như là tích ?1?2 …?? trong đó ?i lấy một trong 3 giá trị 1, ?i, ?̅i. Do đó số đơn thức khác nhau là 3?. suy ra mỗi hàm Bool chỉ có một số hữu hạn công thức đa thức. Để ý rằng nếu ?i ≠ 1, ta nói ?i là một thừa số của ?. Như thế mỗi đơn thức được viết như là tích của tối đa ? thừa số khác nhau.
MẠNG CÁC CỔNG VÀ CÔNG THỨC ĐA THỨC TỐI TIỂU
Trong ví dụ về mạch điện ở §2, ta đã biểu diễn mạch điện dưới dạng một hàm Bool để khảo sát sự phũ thuộc của output ? (có dòng điện chạy qua hay không) theo các input ?, ?, ? (ngắt điện tương ứng đóng hay mở). Bây giờ ta hãy xét bài toán ngược lại: cho trước một hàm Bool ƒ( ?, ?, ?,…). Hãy thiết kế một mạng các thiết bị vật lý cho phép tổng hợp nên hàm Bool ƒ. Ở đây ta không quan tâm đến các thiết bị vật lý cụ thể mà chỉ để ý đến các nối kết chúng trong một mạng để tổng hợp nên hàm Bool. Do Mệnh đề 4.2.2 và 4.2.3, mỗi hàm Bool đều có thể viết thành một công thức trong đó các biến logic (biến Bool) được nối kết lại với nhau bởi các phép toán ?,?, −. Do đó ta cần phải tổng hợp các phép toán trên. Thiết bị để tổng hợp các phép toán này gọi là các cổng được biểu diễn bởi các sơ đồ sau:

Tron các sơ đồ trên, ? và ? là hai tín hiệu vào với 2 trạng thái khác nhau cho phép chúng biểu diễn được các biến logic với hai giá trị 0,1. Ở đầu ra ta cũng có một tín hiêu biểu diễn cho một biến logic phụ thuộc vào các input theo các phép toán ?,?, −.
Ví dụ: để tổng hợp hàm Bool ƒ = ?? ? ?̅?, ta có thể sử dụng mạng với các cổng sau:
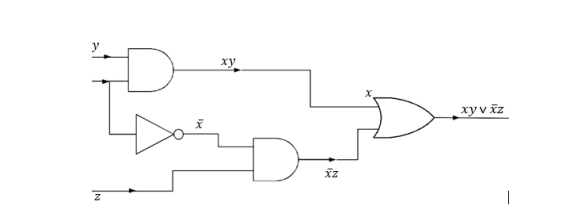
trong đó có hai cổng AND, 1 cổng OR và một cổng NOT. Mặt khác ta cũng c2o thể viết hàm ƒ như sau:
ƒ = ??( ? ? ?̅ ) ? ?̅( ? ? ?̅ ) ?
= ??? ? ???̅ ? ?̅?? ? ?̅?̅?
Đây là dạng nối rời chính tắc của ƒ vì các số hạng đều là từ tối tiểu. nếu sử dung công thức trên để thiết kế một mạng các tổng hợp f, ta phải sử dụng 8 cổng AND và 3 cổng OR, không kể một số cổng NOT.
Vấn đề được đặt ra là làm sao tìm được một công thứ tối ưu để tổng hợp một hàm Bool cho trước.
Bài toán tối ưu đầu tiên là tìm cách giảm số loại cổng từ 3 xuống còn 2, hoặc nếu được chỉ dùng một loại cổng.
Thật vậy, ta có thể tổng hợp cổng OR từ cổng NOT và cổng AND. Thật ra ta có thể đặt hai cổng này chung thành một cổng có tên là NAND với sơ đồ:

Thật vậy, ta có thể tổng hợp cổng OR từ cổng NOT và cổng AND. Thật ra ta có thể đặt hai cổng này chung thành một cổng có tên là NAND với sơ đồ

Từ đó có thể tổng hợp cổng OR mà chỉ dùng cổng NAND như trong bài tập nêu trên. Suy ra mọi hàm Bool đều được tổng hợp mà chỉ dùng cổng NAND ta cũng có thể dùng cổng NOR với sơ đồ sau:
Khi ấy ta cũng chứng minh được mọi hàm Bool đều được tổng hợp mà chỉ sử dụng cổng NOR.
Bài toán tối ưu tiếp theo là tối ưu hóa hai mục tiêu:
- Cực tiểu hóa thời gian châm trễ (delay): tuy thời gian chậm trễ khi đi qua một cổng là nhỏ nhưng nếu tích lũy qua nhiều lớp cổng thì nó trở thành đáng kể, nhất là trong các máy tính có tốc độ cao.
- Cực tiểu hóa số cổng sử dụng
Do thời gian chậm trễ kho đi qua cổng NOT là không đáng kể, dưới đây khi phân tích các mạch ta có thể bỏ qua cổng NOT. Nói cách khác các biến ?̅, ?̅, ?̅, … cũng được xem như là các biến input tương tự như ?, ?, ?,…
Thật ra hai mục tiêu trên không thể đồng thời tối ưu hóa được. Do đó trước hết ta tối ưu hóa theo thời gian. Ta sẽ thiết kế các mạch chỉ có tối đa hai lớp cổng: lớp cổng AND rồi lớp cổng OR hay lớp cổng OR rồi lớp cổng AND. Tuy nhiên trường hợp sau luôn luôn có thể đưa được về trường hợp trước nếu ta xét ƒ.̅ Do đó ta chỉ xét các công thức có dạng OR (?) của các số hạng là AND (?) của từ đơn. Đây chính là các công thức đa thức
Trong lớp các công thức đa thức, ta có một số thuật toán cho phép tìm được công thức đa thức tối tiểu.
Định nghĩa 4.3.1
Xét hai công thức đa thức của hàm Bool ƒ:
ƒ = ?1 ? ?2 ? .... ??? (4.3.1)
ƒ = ?1 ? ?2 ? …? ?? (4.3.2)
Ta nói (4.3.1) đơn giản hơn (4.3.2) nếu tồn tại một đơn ánh ?: { 1,2,…, ?} →{ 1,2,…, ?} sao cho với 1 ≤ i ≤ ? thì số thừa số là từ đơn của ?i không nhiều hơn số thừa số là từ đơn của ??(i) .
Chú ý:
1. Nếu (4.3.1) đơn giản hơn (4.3.2) thì ? ≤ ?
2. Quan hệ “đơn giản hơn” giữa các công thức đa thức của ƒ rõ ràng có tính phản xạ và bắc cầu. Tuy nhiên quan hệ này không phản xứng.
3. Nói rằng (4.3.1) đơn giản hơn (4.3.2) và (4.3.2) đơn giản hơn (4.3.1) có nghĩa là tồn tại các đơn ánh
?: { 1,2,…, ?} → { 1,2,…, ?}
và ?: { 1,2,…, ?} → { 1,2,…, ?}
sao cho ?, ? thỏa Định nghĩa 4.3.1. Khi ấy ?, ? là song ánh và với 1 ≤ i ≤ ? thì số thừa số là từ đơn của ?i không nhiều hơn số thừa số là từ đơn của ??∘?(i) . Do đó nếu gọi ? là số nguyên nhỏ nhất sao cho
và
thì ?i và ?j có thừa số là từ đơn bằng nhau.
Suy ra với 1 ≤ i ≤ ? thì ?i và ??(i) có thừa số là từ đơn bằng nhau. Khi ấy ta nói (4.3.1) và (4.3.2) đơn giản như nhau. Rõ ràng quan hệ đơn giản như nhau là một quan hệ tương đương. Hơn nữa nếu hai công thức đa thức là đơn gản như nhau thì mạng các cổng tổng hợp chúng sẽ sử dụng cùng số cổng AND và cổng OR.
4. Tương tự như trong Chương 3, nếu chuyển qua các lớp tương đương thì quan hệ đơn giản hơn trở thành một thứ tự. Tuy nhiên ta cũng có thể khảo sát trực tiếp các quan hệ chỉ có hai tính chất phản xạ và bắc cầu. ta nói chứng là các quan hệ tiền thứ tự . Đối với quan hệ tiền thứ tự, khái niệm phần tử tối tiểu và tối đại vẫn còn ý nghĩa. Chẳng hạn như một công thức đa thức (?) của hàm Bool ƒ được nói là tối tiểu nếu với bất kỳ công thức đa thức (?) của ƒ “đơn giản hơn” (?) thì (?) và (?) đơn giản như nhau. Bây giờ do tập hợp các công thức đa thức của một hàm Bool ƒ là hữu hạn, ta chứng minh được tương tự như Định lý 3.3.3, cho trước một công thức đa thức (?) của ƒ thì sẽ tồ tại một công thức đa thức tối tiểu (?) của ƒ sao cho (?) đơn giản hơn (?). Cũng như trường hợp các tập hợp có thứ tự, một hàm Bool ƒ có thể có nhiều công thức đa thức tối tiểu.
5. Xét công thức đa thức (4.3.1) của hàm ƒ. Giả sử tồn tại một dơn thức ? sao cho ?1 ? ≺ ƒ. Khi ấy ta có:
ƒ = ? ? ƒ = ( ? ? ?1) ? ?2 ? …? ??
ƒ = ? ? ? 2? …? ?? (4.3.3)
Do ?1 ≺ ? ta có thể viết: ??1 = ?1
Như thế mọi thừa số là từ đơn của ? cũng là một thừa số của ?1 . Hơn nữa do ?1 ≠ ? nên có ít nhất một thừa số là từ đơn của ?1 không xuất hiện trong ?. Khi ấy công thức (4.3.3) rõ ràng đơn giản hơn (4.3.1) nhưng không đơn giản như nhau. Suy ra (4.3.1) không tối tiểu. Ta đã chứng minh.
Mệnh đề 4.3.1
Trong một công thức đa thức tối tiểu, các số hạng là đơn thức tối dại trội bởi ƒ.
Định nghĩa 4.3.2
Một đơn thức tối đại trội bởi hàm Bool ƒ được gọi là một tiền đề nguyên tố của ƒ.
Do Mệnh đề 4.3.1, để tìm công thức đa thức tối tiểu của một hàm Bool ƒ, ta hạn chế tìm kiếm trong các công thức đa thức mà các số hạng là những tiền đề nguyên tố dôi một khác nhau. Các công thức này là rút gịn theo nghĩa sau:
Định nghĩa 4.3.3:
Công thức đa thức (4.3.1) của hàm ƒ được nói là rút gọn nếu với 1 ≤ i ≠ j ≤ ?, thì ?i không phải là ước thật sự của ?j.
Bổ đề 4.3.2: nếu ? và ℎ là hai hàm Bool thì ?ℎ̅ ? ℎ = ? ? ℎ
Chứng minh:
?ℎ̅ ? ℎ = ?ℎ̅ ? ( ?ℎ ? ℎ)
= ?(ℎ̅ ? ℎ) ? ℎ = ? ? ℎ l đpcm
Từ (?1) ta được:
ƒ = ??? ? ?( ? ? ?̅) ?̅ ? ?̅??̅
ƒ = ??? ? ??̅ ? ?̅??̅ (?2)
Tương tự
ƒ = ??? ? ??̅?̅ ? ??̅ (?3)
và
ƒ = ?? ? ??̅?̅ ? ?̅??̅ (?4)
Áp dụng Bổ đề 4.3.2 cho (?2), (?3) và (?4) ta được:
ƒ = ?( ?? ? ?? ?̅??
= ?( ? ? ?)̅ ? ?̅??̅
= ?? ? ??̅ ? ?̅??̅ (?5)
Tương tự
ƒ = ??? ? ??̅ ? ??̅ (?6)
và
ƒ = ?? ? ??̅?̅ ? ??̅ (?7)
Cuối cùng, áp dụng Bổ đề 4.3.2 cho một trong 3 công thức (?5), (?6) hay (?7) ta được:
ƒ = ?? ? ??̅ ? ??̅ (?8)
Tám công thức trên đều là rút gọn và có biểu đồ Hasse:
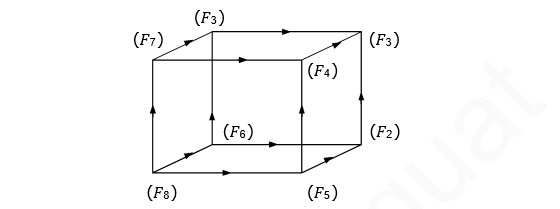
Công thức (?8 ) là công thức đa thức tối tiểu duy nhất nên cũng là công thức đơn giản nhất . Sử dụng công thức (?8 ) để tổng hợp hàm Bool ƒ ta chỉ tốn 3 cổng AND và 2 cổng OR thay vì 8 cổng AND và 3 cổng OR nếu dùng (?1 ). Ta có sơ đồ mạch các cổng ứng với (?8 ) như sau:
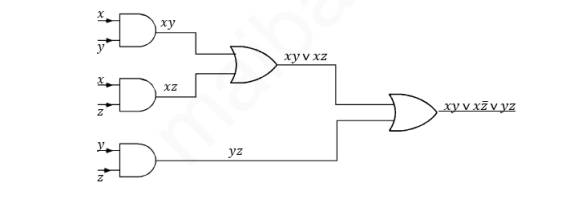 PHƯƠNG PHÁP BIỂU ĐỒ KARNAUGH
PHƯƠNG PHÁP BIỂU ĐỒ KARNAUGH
Phương pháp biểu đồ Karnaugh cho phép tìm nhanh công thức đa thức tối tiểu của hàm Bool 3, 4 biến. Trường hợp 3 biến hoàn toàn tương tự nhưng đơn giản hơn trường hợp 4 biến. Do đó ta tập trung trình bày 4 biến. Nhắc lại một hàm Bool 4 biến là một ánh xạ ?4 → ? nên để có thẻ biểu diễn bằng hình ảnh ta sẽ sử dụng một hình vuông gồm có 16 ô vuông nhỏ để biểu diễn 16 phần tử của ?4. Khi ấy ta có thể biểu diễn một hàm Bool
ƒ: ?4 → ? bằng các gạch chéo các ô ở đó ƒ bằng 1.
Như vậy vấn đề chính là đánh dấu 16 ô của hình vuông tương ứng với các phần tử của ?4. Ta đã biết các phần tử của ?4 có thể được sắp thứ tự theo thứ tự tự điển:
0000,0001,,0010,0011,…,1111
Ta có thể xếp các phần tử của ?4 theo thứ tự lần lượt trên các dòng của hình vuông lớn. tuy nhiên cách này không thuận tiện bằng cách của Veitch và Karnaugh như sau:
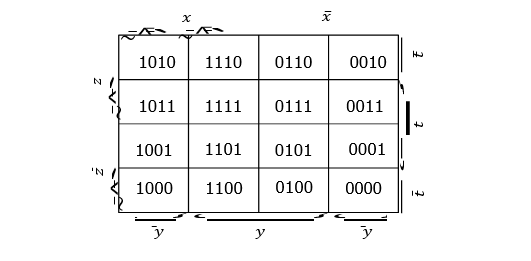 Ở đây ký hiệu ? chỉ cột ở đó biến đầu tiên ? lấy giá trị 1, ?̅ chỉ cột ở đó biến ? lấy giá trị 0. Tương tự cho biến thứ hai ?. Các biến thứ ba và thứ tư ?, ? được gán với các dòng. Ví dụ ở hai dòng đầu biến ? lấy giá trị 1 và 2 dòg nsau biến ? lấy giá trị 0. Tương tự cho biến ?. Cách biểu diễn trên của ?4 rất thuận tiện cho việc biểu diễn các đơn thức. Thật vậy ta nhận xét rằng 2 ô liên tiếp nhau chỉ khác nhau một thành phần , ví dụ ô ở dòng 2 cột 2 và ô ở dòng 2 cột 3 chỉ khác nhau ở thành phần đầu tiên: 1111 và 0111. Mặt khác ô ở dòng 1 cột 1 và dòng 1 cột 4 cũng biểu diễn hai phần tử chỉ khác nhau một thành phần: 1010 và 0010. Ta quy ước rằng các ô này cũng được xem như kề nhau theo nghĩa rộng: 2 ô được nói là kề nhau theo nghĩa rộng nếu sau khi ta cuốn hình vuông theo chiều rộng hoặc chiều ngang tạo thành hình trụ thì hai ô ban đầu sẽ trở thành kề nhau trên hình trụ. Với qui ước trên ta thấy rằng hai ô kề nhau (theo nghĩa thông thường hay nghĩa rộng) khi và chỉ khi chùng biểu diễn hai phần tử của ?4 chỉ khác nhau một thành phần.
Ở đây ký hiệu ? chỉ cột ở đó biến đầu tiên ? lấy giá trị 1, ?̅ chỉ cột ở đó biến ? lấy giá trị 0. Tương tự cho biến thứ hai ?. Các biến thứ ba và thứ tư ?, ? được gán với các dòng. Ví dụ ở hai dòng đầu biến ? lấy giá trị 1 và 2 dòg nsau biến ? lấy giá trị 0. Tương tự cho biến ?. Cách biểu diễn trên của ?4 rất thuận tiện cho việc biểu diễn các đơn thức. Thật vậy ta nhận xét rằng 2 ô liên tiếp nhau chỉ khác nhau một thành phần , ví dụ ô ở dòng 2 cột 2 và ô ở dòng 2 cột 3 chỉ khác nhau ở thành phần đầu tiên: 1111 và 0111. Mặt khác ô ở dòng 1 cột 1 và dòng 1 cột 4 cũng biểu diễn hai phần tử chỉ khác nhau một thành phần: 1010 và 0010. Ta quy ước rằng các ô này cũng được xem như kề nhau theo nghĩa rộng: 2 ô được nói là kề nhau theo nghĩa rộng nếu sau khi ta cuốn hình vuông theo chiều rộng hoặc chiều ngang tạo thành hình trụ thì hai ô ban đầu sẽ trở thành kề nhau trên hình trụ. Với qui ước trên ta thấy rằng hai ô kề nhau (theo nghĩa thông thường hay nghĩa rộng) khi và chỉ khi chùng biểu diễn hai phần tử của ?4 chỉ khác nhau một thành phần.
Bây giờ để biểu diễn một hàm Bool 4 biến ƒ, ta sẽ gạch chéo các ô của hình vuông lớn tương ứng với các điểm của ?4 ở đó ƒ bằng 1. Ta nói hình vẽ ấy là biểu đồ Karnaugh của hàm Bool ƒ. Ví dụ như hình vẽ dưới đây chỉ biểu đồ Karnagh của hàm Bool 4 biến:
ƒ = ???? ? ????̅ ? ?̅??? ? ?̅??̅? ? ?̅??̅?̅ ? ?̅?̅?̅?
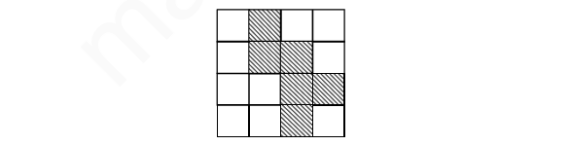
Nhận xét rằng hàm Bool ƒ chính là các hàm đặc trưng của tập hợp gạch chéo trong biểu đồ Karnaugh. Do đó sử dụng đẳng cấu giữa 2 đại số Bool ?( ?4) và 2?4 ta có:
Mệnh đề 4.4.1:
Với mọi hàm Bool 4 biến ƒ, ?:
i. Biểu đồ Karnaugh của ƒ là tập hợp con của biểu đồ Karnaugh của ? khi và chỉ khi ƒ ≺ ?
ii. Biểu đồ Karnaugh của ƒ ? ? (tương ứng ƒ ? ?) là hợp (tương ứng giao) của các biểu đồ Karnaugh của ƒ và ?.
iii. Biểu đồ Karnaugh của ƒ̅ là phần bù của biểu đồ Karnaugh của ƒ.
Chú ý:
1. Sử dụng Mệnh đề 4.4.1 ta có thể vẽ được biểu đồ Karnaugh của một hàm Bool nếu biết bảng chân trị của nó hoặc nếu biết được một công thức biểu diễn hàm Bool dưới dạng một biểu thức theo các biến và các phép toán ?,?, −.
2. Ngược lại nếu biết được biểu đồ Karnaugh của hàm Bool ƒ, ta có thể đọc ngay từ đó dạng nối rời chính tắc: các từ tối tiểu trội bởi ƒ chính là các hàm đặc trưng của mỗi ô nằm trong biểu đồ Karnaugh. Hơn nữa, công thức cho từ tối tiểu như là tích của bốn từ đơn được đọc ngay triong biểu đồ Karnaugh khi xem các dòng và cột chứa ô đang xét: ví dụ như từ đơn ứng với ô ở dòng 3 cột 2 là ???̅? thì các dòng và cột chứa ô này là ?, ?, ?̅ và ?.
3. Hai từ tối tiểu ứng với hai ô kề nhau ( theo nghĩa thông thường hoặc nghĩa rộng) hỉ khác nhau một thừa số là từ đơn, nên ta có thể dùng luật phân bố để đặt thừa số chung trong tổng Bool của chúng và được một đơn thức có 3 thừa số là từ đơn. Ví dụ như:
???? ? ????̅ = ???( ? ? ? = ???
có biểu đồ Karnaugh là một hình chữ nhật theo nghĩa rộng gồm hai ô liên tiếp nhau 1110 và 1111.
Tổng quát hơn ta có:
Mệnh đề 4.4.2:
Biểu đồ Karnaugh của một đơn thức có dạng tích của ?( 1 ≤ ? ≤ 4) từ đơn là một hình chũ nhật (theo nghĩa rộng) gồm 24−? ô, mà ta gọi là các tế bào.
Ví dụ:
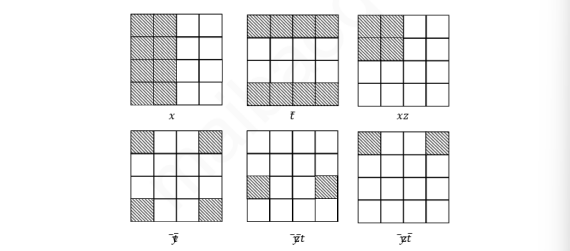
Do Mệnh đề 4.4.1 và 4.4.2, các tiền đề nguyên tố của một hàm Bool 4 biến có biểu đồ Karnaugh là một tế bào tối đại nằm trong biểu đồ Karnaugh của ƒ. Ta nói các tế bào này là tế bào lớn của biểu đồ Karnaugh của ƒ. Như vậy việc tìm công thức đa thức tối tiểu của ƒ đưa về việc giải quyết hai vấn đề:
- Tìm tất cả các tế bào lớn nằm trong biểu đồ Karnaugh của ƒ.
- Tìm một phép phủ tối tiểu biểu đồ Karnaugh của ƒ bằng các tế bào lớn, nghĩa là một họ tế bào lớn có hợp là biểu đồ Karnaugh của ƒ sao cho khi rút bớt một tế bào lớn thì họ còn lại không phủ kín biểu đồ Karnaugh của ƒ. Từ đó ta được một thuật toán để tìm công thức đa thức tối tiểu.
Thuật toán: gồm 4 bước
Bước 1: chỉ ra tất cả các tế bào lớn của biểu đồ Karnaugh của ƒ.
Sau bước 1 ta sẽ phủ dần biểu đồ Karnaugh bằng các tế bào lớn cho đến khi phủ kín
Bước 2: Nếu tồn tại một ô chỉ nằm trong một tế bào lớn duy nhất, ta chọn ra tế bào này để phủ. Trong phần còn lại của biểu đồ Karnaugh, nếu có một ô chỉ nằm trong một tế bào lớn duy nhất, ta chọn ra tế bào này để phủ, và lặp lại bước 2 cho đến khi không còn ô nào có tính chất trên.
Bước 3: nếu các tế bào lớn chọn trong Bước 2 đã phủ kín biểu đồ Karnaugh của ƒ ta qua thẳng Bước 4. Nếu không, chọn ra một ô còn lại. Trong số các tế bào lớn chứa ô này ta chọn ra một ô tùy ý dể thêm vào phép phủ và cứ tiếp tục như trên cho phần còn lại cho đến khi phủ kín biểu đồ Karnaugh của ƒ.
Bước 4: ở bước này ta đã chọn được một số tế bào lớn phủ kín biểu đồ Karnaugh của ƒ. Do trong Bước 3 có sự lựa chọn tùy tế bào lớn chứa một ô , ta thường có nhiều hơn một phép phủ. Trong số phép phủ nhận được, loại bỏ các phép phủ không tối tiểu. Sau cùng các phép phủ còn lại cho ta một công thức đa thức của ƒ mà ta còn phải so sánh chúng theo Định nghĩa 4.3.1: loại bỏ những công thức có một công thức khác trong số đó thực sự đơn giản hơn nó. Các công thức còn lại chính là công thức đa thức tối tiểu phải tìm.
Chú ý:
1. Nếu Bước 3 được bỏ qua thì không có sự lựa chọn tùy ý. Trong trường hợp any2 ta được một phép phủ duy nhất tương ứng với công thức đa thức tối tiểu duy nhất.
2. Để thuận tiện cho việc xem xét ta gạch chéo mỗi tế bào lớn được chọn cho đến khi phần gạch chéo trùng với biểu đồ Karnaugh của ƒ. Đương nhiên hai cách chọn khác nahu sẽ dẫn đến hai quá trình phủ khác nhau và cho ta hai công thức khác nhau.
PHƯƠNG PHÁP THỎA THUẬN
Nhắc lại hai bài toán chính để tìm công thức đa thức tối tiểu của một hàm Bool ƒ:
- Tìm tất cả các tiền đề nguyên tố của ƒ
- Tìm cách biểu diễn ƒ như là tổng tối tiểu của các tiền đề nguyên tố Để giải quyết bài toán 5.1 ta sẽ dùng phương pháp thỏa thuận
Định nghĩa 4.5.1
Giả sử ? là một trong các biến Bool và ?1, ?2 là hai đơn thức không chia hết cho cả ? lẫn ?̅. Khi ấy được nói là thỏa thuận giữa hai đơn thức ??1 và ?̅?2.
Chú ý: nếu có một biến thứ hai ? sao cho ?1 chia hết cho ? (hoặc ?̅) và ?2 chia hết cho ?̅ (hoặc ?), khi ấy thỏa thuận ?1?2 rõ ràng bằng 0. Do đó cho trước 3 đơn thức có 3 trường hợp có thể xảy ra:
Trường hợp 1: không tìm được thỏa thuận của chúng vì không có biến ? nào như trong Định nghĩa 4.5.1
Trường hợp 2: thỏa thuận của chúng bằng 0 vì có ít nhất hai biến Bool thỏa Định nghĩa 4.5.1
Trường hợp 3: chỉ có một biến Bool thỏa Định nghĩa 4.5.1 và do đó thỏa thuận của hai đơn thức cho trước là một đơn thức (≠ 0)
Ví dụ:
1. ?? ?à ??̅ không có thỏa thuận
2. ??̅? ?à ??̅? có thỏa thuận bằng 0
3. ??̅? ?à ?? có thỏa thuận là ???
Định lý 4.5.1
Thỏa thuận của haqi đơn thức luôn luôn đượ trội bởi tổng Bool của hai đơn thức ấy.
Chứng minh: Xét hai đơn thức ??1 và ?̅?2 với thỏa thuận ?1?2 ta có:
?1?2 = ?1?2( ? ? ?̅) = ??1?2 ? ?̅?1?2
Suy ra:
?1?2 ? ??1 ? ?̅?2 = ( ??1?2 ? ??1) ? ( ?̅?2 ??̅?2?1)
= ??1 ? ?̅?2
Nghĩa là ?1?2 ≺ ??1 ≺ ?̅?2 l đpcm
Với khái niệm thỏa thuận ta có phương pháp sau để xác định tất cả các tiền đề nguyên tố của một hàm Bool ƒ.
Bước 1: Viết ƒ dưới dạng công thức thu gọn tùy ý (dạng nối rồi chính tắc chẳng hạn):
Đặt ➚ = { ?1, ?2,…, ??}
ƒ = ?1 ? ?2 ? …? ??
Gọi ࣰ là danh sách các biến theo một thứ tự nhất định nhưng tùy ý.
Bước 2: Trong Bước 2 ta sẽ cập nhật dần ➚ theo từng biến trong ࣰ như sau:
i. Giả sử ? là một biến trong ࣰ mà ta đã xét tới với ➚ đã được cập nhật theo các biến trước ?. Ta phần hoạch ➚ thành 3 phần (rời nhau):
- ? gồm các đơn thức chia hết cho ?
- ? gồm các đơn thức chia hết cho ?̅
- gồm các đơn thức không chia hết cho ? lẫn ?̅
ii. Nếu ? = ∅ hay ? = ∅ ta sẽ xét biến kế tiếp ?. Nếu không, ta thêm vào ➚ tất cả các thỏa thuận của một đơn thức thuộc ? và một đơn thức thuộc ?.
iii. Mỗi lẩn thêm một phần tử mới vào ➚ ta phải duyệt lại và loại bớt những phần tử được trội thực sự bởi một phần tử khác (kể cả phần tử mới thêm vào).
Bước 3: Sau khi đã duyệt tất cả các biến trong ࣰ ta có:
Định lý 4.5.2:
Tập hợp ➚ sau cùng trong Bước 3 chính là tập hợp tất cả các tiền đề nguyên tố của ƒ.
Chứng minh:
Gọi ? là số biến trong ࣰ, và một ? là một tiền đề nguyên tố bất kỳ của ƒ, ta chứng minh tập hợp ➚ sau cùng sẽ chứa ? bằng quy nạp trên ?.
Gọi ? là biến đầu tiên trong danh sách ࣰ và ?, ?, ✔ là các tập hợp tương ứng như trong i).
Trường hợp 1: ? không chia hết cho ? lẫn ?̅, ta có:
?? ≺ ( Ç ?) ? ? (Ç??) ? (Ç ?) ?
Ở đây kí hiệu Ç ? dùng để chỉ tổng Bool của tất cả các phần tử của A. Các ký hiệu khác cũng tương tự. để ý rằng nếu ? ∈ ? thì ? chia hia hết cho ?̅ nên ?? = 0. Do đó:
?? ≺ (Ç ?/ ?) ? ? (Ç ?) ?
Cho ? = 1 ta được
? ≺ (Ç ?/ ?) ? (Ç ?)
Tương tự ta có
? ≺ (Ç?/ ?̅) ? (Ç ?)
Suy ra
? ≺ ( Ç ( ?/ ?) ( ?/ ?̅) ) ?∈✔
Giả sử ➚ đã được cập nhật theo biến ? như trong Bước 2 ở trên. Gọi ➚′ là tập hợp con của ➚ gồm các đơn thức không chia hết cho ? lẫn ?̅. Gọi ƒ′ là tổng Bool của các đơn thức trong ➚′ xem như hàm Bool theo các biến trong ࣰ′ = ࣰ\ { ?} . Rõ ràng ? là một tiền đề nguyên tố của ƒ′ nên theo giả thiết quy nạp, sau khi cập nhật theo biến cuối cùng trong
ࣰ′, ➚′ chứa ?. Nhưng tập hợp ➚′ sau cùng là tậph ợp con của tập hợp ➚ sau khi cập nhật theo biến sau cùng của ࣰ′, vì trong quá trình cập nhật theo các biến của ࣰ′, các đơn thức của ➚ bị loại đi cũng chính là các đơn thức của ➚′ bị loại đi hoặc là các đơn thức chia hết cho ? hoặc ?̅. Nói tóm lại ta đã chứng minh được tậph ợp ➚ sau cùng chứa ?.
Trường hợp 2: ? chia hết cho ? hay ?̅. Ta có thể giả sử ? chia hết cho ? vì trường hợp còn lại chứng minh tương tự.
Gọi ?, ?, ✔ là 3 tập hợp tạo thành phân hoạch của ➚ tương ứng với biến ? như trong Bước 2. Cho ? = 1 ta được:
?/ ? ≺ (Ç( ?/ ?) ) ? (Ç ?)
Suy ra
? ≺ (Ç ?) ? ? (Ç ?)
≺ (Ç ?) ? (Ç ?) = ƒ
Ứng với mỗi hàm Bool ? theo các biến trong ࣰ, ta liên kết một hàm Bool ?̅ với các biến trong ࣰ′ = ࣰ\ { ?} bằng cách cho ? = 1. Đặt ➚′ = ? ? ✔. Khi ấy ? ⟼ ?̅ là một song ánh giữa ➚′ và một tập hợp ➚̅′ các từ đơn theo các biến trong ࣰ′ vì không có phần tử nào của ✔ là ước của một phần tử của ? (công thức đa thức ban đầu của ƒ là rút gọn).
Ta có công thức đa thức rút gọn:
ƒ = (Ç ?̅) ? (Ç ?)
?∈? ?∈✔
Hơn nữa tương ứng ? ⟼ ?̅, nếu thu hệp trên tập ➚′ đã được cập nhật đối vối biến sau cùng, cũng là một song ánh giữa tập hợp này và tập hợp ➚̅′ đã được cập nhật theo biến sau cùng đối với hàm ƒ̅′, vì nếu có ?̅1 = ?̅2 với ?1 ≠ ?2 thì một trong hai đơn thức ?1, ?2 là tích của đơn thức kia và ? nên đã được loại trong quá trình cập nhật.
Rõ ràng ?̅ ≺ ƒ,
giả sử tồn tại đơn thức ?̅′ theo các biến trong ࣰ′ sao cho:
?̅ ≺ ?̅′ ≺ ƒ̅′
Ta có:
? = ??̅ ≺ ??̅′ ≺ ?ƒ̅′ = (Ç ??̅) ? ? (Ç ?) ≺ ƒ
?∈? ?
Suy ra ?̅ = ?̅′, nghĩa là ?̅ là tiền đề nguyên tố của ƒ̅′
Như thế theo giả thiết quy nạp, ➚̅′, sau khi cập nhật theo biến cuối cùng, sẽ chứa ?̅ . Tương tự như trong Trường hợp 1, ta thấy tập hợp ➚ sau khi cập nhật đối với biến cuối cùng, sẽ chứa ➚′.
Suy ra ? ∈ ➚
Cuối cùng do cách cập nhật các đơn thức, trong đơn thức nào trong ➚ được trội thực sự bởi một đơn thức khác, nghĩa là các phần tử của ➚ đều là tiền đề nguyên tố của ƒ. l đpcm
Bài toán phủ:
Tìm một họ ➚0 các tiền đề nguyên tố của ƒ sao cho:
i. Mỗi từ tối tiểu trội bởi ƒ được trội bởi một tiền đề thuộc ➚0
ii. Họ ➚0 là từ tối tiểu, nghĩa là nếu rút bớt một phần tử thì phần còn lại không thỏa i)
Gọi ➚ = {?1,…, ??} là tập hợp tất cả các tiền dề nguyên tố của ƒ mà ta tìm được khi giải bài toán 5.1
Ta đưa vào các biến Bool ?1, ?2,…, ?? và tgiet61 lập một hệ phương trình Bool theo các biến Bool như sau:
Với mỗi từ tối tiểu ➚ trội bởi ƒ, gọi ?i1 , ?i2 ,…, ?ik là tất cả các tiền đề nguyên tố của ƒ trội ?. Khi ấy ta có một phương trình: ?i1 ? ?i2 ? …? ?ik = 1
Cho ? chạy khắp các từ tối tiểu trội bởi ƒ, ta được một hệ ? phương trình trong đó ? là số các từ tối tiểu trội bởi ƒ. Giải hệ phương trình Bool trên ta được các nghiệm là bộ ?:
Trong đó ?1, ?2,…, ?? là các giá trị cố định bằng 1 hoặc tùy ý. Với các ?i = 1 ta có ?i = 1, nghĩa là tiền đề nguyên tố ?i được chọn để phủ ƒ. Để giải hệ phương trình Bool có dạng trên, ta thực hiên các bước sau:
Bước 1: loại bỏ các phương trình trùng lắp, nói cách khác giả sử có hai phương trình có dạng:
?i1 ? ?i2 ? …? ?ik = 1
và ?j1 ? ?j2 ? …? ?jℎ = 1
sao cho { i1, i2,…, ik} ⊂ { j1, j2,…, jℎ}
Khi ấy phương trình thứ hai là hệ quả của phương trình đầu và do đó có thể được loại bỏ
Bước 2: Vì hệ phương trình đồng thời nghiệm đúng, ta thấy nó tương đương với một phương trình duy nhất có vế trái là tích của tất cả các vế trái và vế phải bằng 1 Dùng luật phân bố khai triển vế trái và đưa nó về dạng một công thức đa thức.
Bước 3: Loại bỏ các đơn thức dư thừa, nghĩa là nó là bội của một đơn thức khác. Nói cách khác đưa vế trái của phương trình đã biến đổi ở Bước 2 về dạng một công thức đa thức rút gọn. Ở đây lưu ý rằng các đơn thức đều là tích của một số biến, không có thừa số đơn nào là phần bù của biến. Phương trình trở thành: ?1 ? ?2 ? …? ?? = 1
Bước 4: các lời giải là:
?1 = 1
hay ?2 = 1
…
hay ?? = 1
Mỗi ?i là tích của một số biến, nên lời giải tương ứng chính là các tiền đề nguyên tố tương ứng với biến đó.
Ví dụ: trong ví dụ 2 ở trên, ta có 4 tiền đề nguyên tố ?1 = ?̅??, ?2 = ?̅??, ?3 = ??̅?, ?4 = ???̅, và 5 từ tối tiểu ?1 = ?̅?̅??, ?2 = ?̅???, ?3 = ?̅??̅?, ?4 = ???̅?, ?5? = ??̅?̅.
Ta có hệ 5 phương trình:
a1 =1
a1 v a2=1
a2 v a3=1
a3 v a4=1
Phương trình thứ hai là hệ quả của phương trình đầu và phương trình thứ 4 là hệ quả của phương trình cuối: loại bỏ chúng và lấy tích ta được phương trình duy nhất:
?1( ?2 ? ?3) ?4 = 1
Khai triển ta được: ?1?2?4 ? ?1?3?4 = 1
Do đó ta có hai lời giải:
?1?2?4 = 1
hay ?1?3?4 = 1
Nói cách khác ta có hai công thức đa thức:
ƒ = ?1 ? ?2 ? ?4 = ?̅?? ? ?̅?? ? ???̅
và ƒ = ?1 ? ?3 ? ?4 = ?̅?? ? ??̅? ? ???̅
Cả hai đều là công thức đa thức tối tiểu.
Xem thêm:
Tóm tắt lý thuyết toán cao cấp
Tóm tắt lý thuyết toán rời rạc Chương 1: Cơ sở Logic
Tóm tắt lý thuyết toán rời rạc Chương 2: Phương pháp đếm
Tóm tắt lý thuyết toán rời rạc Chương 3: Quan hệ
Tóm tắt lý thuyết toán rời rạc Chương 4: Đại số Bool và hàm Bool
Việc làm dành cho sinh viên:
Việc làm thực tập sinh kiểm toán
Việc làm gia sư các môn cập nhật theo ngày mới nhất
Việc làm thêm nhân viên phục vụ nhà hàng/ quán cafe dành cho sinh viên
Việc làm cộng tác viên kế toán
Mức lương của Thực tập sinh kế toán là bao nhiêu?














