Phương pháp đếm | Tóm tắt lý thuyết Toán rời rạc | Đại học Ngoại Ngữ Tin Học TP Hồ Chí Minh

PHƯƠNG PHÁP ĐẾM

TẬP HỢP

1. Khái niệm

Trong chương trước ta đã sử dụng khái niệm tập hợp trong một số ví dụ, đặc biệt trong định nghĩa của các lượng từ. Trong chương này ta tiếp tục sử dụng khái niệm tập hợp theo nghĩa trực quan: đó là những đối tượng được nhóm lại theo một tính chất nào đó. Nếu

𝑎 là một phần tử của tập hợp 𝐴, ta viết 𝑎 ∈ 𝐴. Trong trường hợp ngược lại ta viết 𝑎 ∉ 𝐴.

Ở đây khái niệm “tính chất” được hiểu theo một nghĩa hết sức rộng rãi. Thường thì nó biểu hiện bởi một vị từ 𝑝( 𝑥) theo một biến 𝑥 ∈ ࣯. Khi ấy tập hợp tất cả các phần tử

𝑥 ∈ ࣯ sao cho 𝑝( 𝑥) đúng được kí hiệu bởi:

𝐴 = { 𝑥 ∈ ࣯⁄𝑝( 𝑥) }, được gọi là tập hợp vũ trụ. Nếu ࣯ hiểu ngầm thì 𝐴 có thể viết:

𝐴 = { 𝑥/ 𝑝( 𝑥) }

Ví dụ:

1. A = { x ∈ N/x là số nguyên tố}

2. A = { x ∈ Z/x² < 5}

Trong ví dụ 2, ta có thể chỉ ra tất cả các phần tử của 𝐴: -2, -1, 0, 1, 2. Ta viết

𝐴 = { −2, −1, 0, 1, 2}

Ta nói 𝐴 được mô tả bằng cách liệt ra tất cả các phần tử. Cũng thế 𝐵 = { 𝑥 ∈ 𝑁/ 𝑥 ≤ 𝑛} có thể được mô tả bằng cách liệt kê các phần tử:

𝐵 = { 0, 1,…, 𝑛}

Với phương pháp mô tả bằng cách liệt kê các phần tử, một tập hợp có thể là:

𝐴 = { 1, 2, 97, 100}

Khi này không nhất thiết các phần tử được nhóm lại theo một tính chất cụ thể nào.

Chú ý rằng tập hợp { 𝑥 ∈ 𝑁/ 𝑥2 < 0} không có phần tử nào cả. Ta nói nó là tập hợp rỗng và kí hệu bởi ∅.

Giả sử 𝐴, 𝐵 là 2 tập hợp con của tập hợp vũ trụ ࣯, ta nói 𝐴 là tập hợp con của 𝐵

(hay 𝐴 được bao hàm trong 𝐵 hay 𝐵 bao hàm 𝐴) nếu:

∀𝑥 ∈ ࣯,( 𝑥 ∈ 𝐴) ⟺ ( 𝑥 ∈ 𝐵)

Sử dụng các phép nối trên mệnh đề và vị từ, ta có thể định nghĩa các phép toán hợp (𝖴), giao (∩) và phần bù trên tập hợp.

Định nghĩa 2.1.1:

Giả sử 𝐴, 𝐵 là tập hợp con của tập hợp vũ trụ ࣯. Khi ấy

𝐴 𝖴 𝐵 = { 𝑥 ∈ $\underset{\infty }{\circ }$ / ( 𝑥 ∈ 𝐴) 𝗏 ( 𝑥 ∈ 𝐵) }

𝐴 ∩ 𝐵 = { 𝑥 ∈ $\underset{\infty }{\circ }$/ ( 𝑥 ∈ 𝐴) 𝖠 ( 𝑥 ∈ 𝐵) }

$\overline{A}$ = $\underset{\infty }{\circ }$\𝐴 =  { 𝑥 ∈ $\underset{\infty }{○}$/ 𝑥 ∉ 𝐴}

$\overline{A}$ được gọi là phần bù của 𝐴 (trong $\underset{\infty }{o}$). 

Định lý 2.1.1 :

𝐴, 𝐵, 𝐶 là các tập con tùy ý của ࣯$\underset{\infty }{o}$ta có:

1. Tính giao hoán

2. Tính kết hợp

$$\begin{gathered} \mathrm{A}\cup (\mathrm{B}\cup \mathrm{C})=(\mathrm{A}\cup \mathrm{B})\cup \mathrm{C} \\ \mathrm{A}\cap (\mathrm{B}\cap \mathrm{C})=(\mathrm{A}\cap \mathrm{B})\cap \mathrm{C} \end{gathered}$$

3. Luật De Morgan

$$\begin{gathered} \overline{A\cup B}=\overline{A}\cap \overline{B} \\ \overline{A\cap B}=\overline{A}\cup \overline{B} \end{gathered}$$

4. Tính phân bố

$$\begin{gathered} A\cup (B\cap C)=(A\cap B)\cap (A\cup C) \\ A\cap (B\cup C)=(A\cap B)\cup (A\cap C) \end{gathered}$$

Phần tử trung hòa:

$$\begin{gathered} A\cup \varnothing =A \\ A\cap \underset{\infty }{o}=A \end{gathered}$$

5. Phần bù:

 $$\begin{gathered} A\cup \overline{A}=\underset{\infty }{o} \\ A\cap \overline{A}=\varnothing \end{gathered}$$

Do tính kết hợp ta có thể dùng 𝐴 𝖴 𝐵 𝖴 𝐶 để chỉ 𝐴 𝖴 ( 𝐵 𝖴 𝐶) hay ( 𝐴 𝖴 𝐵) 𝖴 𝐶. Cũng thế, cho trước 𝑛 tập hợp 𝐴1 𝖴 𝐴2 𝖴 …𝖴 𝐴𝑛 không phụ thuộc vào thứ tự đặt dấu ngoặc.

Ta cũng viết

$\underset{i=1}{\overset{n}{\cup A_i}}=A_1\cup A_2\cup ...\cup A_n$

Tương tự

$\underset{i=1}{\overset{n}{\angle A_i}}=A_1\cup A_2\cup ...\cup A_n$

ÁNH XẠ

1. Định nghĩa 2.2.1

i. Một ánh xạ ƒ từ tập hợp 𝐴 vào tập hợp 𝐵 là phép tương ứng liên kết với mỗi phần tử 𝑥 của 𝐴 một phần tử duy nhất 𝑦 của 𝐵 mà ta kí hiệu là ƒ( 𝑥) và gọi là ảnh của 𝑥 bởi ƒ. Ta viết:

ƒ: 𝐴 ⟶ 𝐵

𝑥 ⟼ ƒ( 𝑥)

ii. Hai ánh xạ ƒ, 𝑔 từ 𝐴 vào 𝐵 được nói là bằng nhau nếu:

∀𝑥 ∈ 𝐴, ƒ( 𝑥) = 𝑔( 𝑥)

Định nghĩa 2.2.2:

i. Nếu 𝐸 là một tập hợp con của 𝐴 thì ảnh của 𝐸 bởi ƒ là tập hợp:

ƒ( 𝐸) = { 𝑦є𝐵/ ∃𝑥 ∈ 𝐸, 𝑦 =  ƒ( 𝑥) }

Ta cũng viết:

ƒ( 𝐸) = { ƒ( 𝑥) / 𝑥 ∈ 𝐸}

ii. Nếu 𝐹 là một tập hợp con của 𝐵 thì ảnh ngược (tạo ảnh) của 𝐹 là tập hợp

ƒ−1( 𝐹) = { 𝑥 ∈ 𝐴/ ƒ( 𝑥) ∈ 𝐹}

Chú ý:

1. Nếu 𝑦є𝐵 thì ta viết ƒ−1( { 𝑦}) =  ƒ−1( 𝑦) .

2. Nếu ƒ−1( 𝑦) = ∅ thì 𝑦 không nằm trong ảnh ƒ( 𝐴) của 𝐴.

3. Nếu ƒ−1( 𝑦) = {𝑥}, thì 𝑥 là phần tử duy nhất có ảnh là 𝑦.

Định nghĩa 2.2.3:

Gọi ƒ là 1 ánh xạ từ tập hợp 𝐴 vào tập hợp 𝐵. Khi ấy ta nói

i. ƒ là toàn ánh nếu ƒ( 𝐴) = 𝐵

ii. ƒ là đơn ánh nếu hai phần tử khác nhau bất kỳ của 𝐴 có ảnh khác nhau:

∀𝑥, 𝑥′ ∈ 𝐴, 𝑥 ≠ 𝑥′ ⟹ ƒ( 𝑥) ≠ ƒ( 𝑥′)

iii. ƒ là song ánh nếu nó đồng thời là đơn ánh và toàn ánh.

Chú ý: nếu ƒ là song ánh từ 𝐴 lên 𝐵, ta viết:

ƒ: 𝐴 ⟷ 𝐵

Khi ấy với 𝑦 ∈ 𝐵 tùy ý, có phần tử duy nhất 𝑥 ∈ 𝐴 sao cho ƒ( 𝑥) = 𝑦. Như thế tương ứng 𝑦 ⟼ 𝑥 là 1 ánh xạ từ 𝐵 vào 𝐴 mà ta kí hiệu là ƒ⁻¹ :   

$$\begin{gathered} B\to A \\ y\to f^{-1}\left(y\right)=x \end{gathered}$$

Với f(x) = y

Ta có:

ƒ(ƒ⁻¹( 𝑦) )          ∀𝑦 ∈ 𝐵                            ( 2.2.1)

ƒ⁻¹(ƒ( 𝑥) )           ∀𝑥 ∈ 𝐴                            ( 2.2.2)

Giả sử 𝑎, 𝑏 là hai số thực sao cho 𝑎 ≠ 0. Khi ấy f(x) = ax+b và xác định một song ánh giữa 𝑅 và 𝑅. Ánh xạ ngược của nó là

ƒ⁻¹: 𝑅 ⟶ 𝑅

𝑦 ⟼ 𝑎⁻¹𝑦 − 𝑎⁻¹𝑏

Định nghĩa 2.2.4:

Cho hai ánh xạ

ƒ: 𝐴  ⟶ 𝐵 và 𝑔: 𝐵  ⟶ 𝐶

Ánh xạ hợp ℎ là ánh xạ từ 𝐴 vào 𝐶 xác định bởi:

ℎ ∶ 𝐴 ⟶ 𝐶

𝑥 ⟼ ℎ( 𝑥) = 𝑔(ƒ( 𝑥) )

Ta viết:

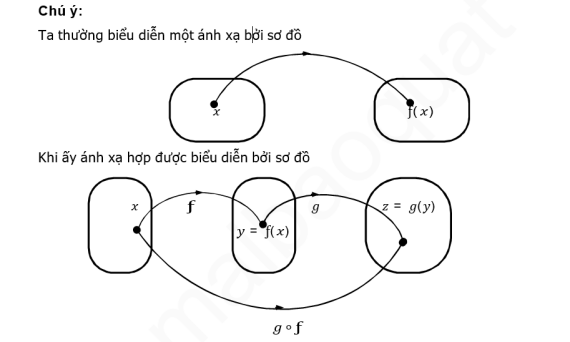
Ký hiệu i𝑑_AE là ánh xạ 𝐴 ⟶ 𝐴 sao cho

i𝑑_AE( 𝑥) = 𝑥       ∀𝑥 ∈ 𝐴

Ta nói i𝑑_Æ là ánh xạ đồng nhất của 𝐴. tương tự gọi i𝑑_𝐵 là ánh xạ đồng nhất của 𝐵. Khi ấy (2.2.1) và (2.2.2) trở thành

và ƒ⁻¹ ∘ ƒ = i𝑑_Æ

Định lý 2.2.1 :

Giả sử ƒ là một ánh xạ từ 𝐴 vào 𝐵, 𝐸₁ và 𝐸_2 là hai tập con tùy ý của 𝐴, 𝐹₁ và 𝐹₂ là hai tập con tùy ý của 𝐵. Ta có:

• ƒ( 𝐸₁ 𝖴 𝐸₂) = ƒ( 𝐸₁) 𝖴 ƒ( 𝐸₂)
• ƒ( 𝐸₁ ∩ 𝐸₂) ⊂ ƒ( 𝐸₁) ∩ ƒ( 𝐸₂)
• ƒ⁻¹( 𝐹₁ 𝖴 𝐹₂) = ƒ⁻¹( 𝐹₁) 𝖴 ƒ( 𝐹₂)
• ƒ⁻¹( 𝐹₁ ∩ 𝐹₂) = ƒ⁻¹( 𝐹₁) ∩ ƒ⁻¹( 𝐹₂)

Chứng minh: ta chỉ chứng minh i), các phần còn lại được lý luận tương tự. Ta có:

𝑦 ∈ ƒ( 𝐸₁ 𝖴 𝐸₂)     ⟺        ∃𝑥 ∈ 𝐸₁ 𝖴 𝐸₂, 𝑦 = ƒ( 𝑥)

(𝑦 ∈ ƒ( 𝐸₁)) 𝗏 (𝑦 ∈ ƒ( 𝐸₂))

𝑦 ∈ ƒ( 𝐸₁) 𝖴 ƒ( 𝐸₂)

Chú ý: bao hàm trong ii) có thể là ngặt trong ví dụ sau cho thấy. Xét ƒ: 𝑍 ⟶ 𝑍 xác định bởi:

ƒ( 𝑥) =  |𝑥|,  ∀𝑥 ∈ 𝑍

Lấy 𝐸1 = 𝑍+, 𝐸2 = 𝑍−. Ta có 𝐸1 ∩ 𝐸2 = ∅ nên ƒ( 𝐸1 ∩ 𝐸2) = ƒ( ∅) = ∅. Trong khi đó ƒ( 𝐸1) = ƒ( 𝐸2) = 𝑍+ nên ƒ( 𝐸1) ∩ ƒ( 𝐸2) ≠ ∅.

PHÉP ĐẾM

Trước hết ta nhận xét rằng phép đếm các phần tử của một tập hợp 𝐴 là một thủ tục gồm có nhiều bước:

Bước 0: Nếu $A=\varnothing$ ta nói số phần tử của A bằng 0. Nếu không ta qua bước 1

Bước 1: Chọn tùy ý một phần tử $a\in A$ rồi gán a tương ứng với phần tử $A=\left\{a\right\}$ ta nói A  là một phần tử, nếu không ta qua bước 2

Bước2: do 𝐴 ≠{ 𝑎}, tồn tại một phần tử 𝑏∈𝐴và 𝑏≠𝑎. Ta gán b tương ứng với phầntử 2 ∈ 𝑁. Nóicáchkhácta có một song ánh { 𝑎, 𝑏} ⟷ { 1,2}. Nếu 𝐴 ={ 𝑎, 𝑏} ta nói 𝐴 có haiphầntử.Nếukhông,taquaBước3.

Cứ tiếp tục thủ tục như trên. Hai trường hợp có thể xảy ra

Trường hợp 1: thủ tục dừng ở một Bước 𝑛 nào đó, nghĩa là tồn tại một songánhgiữa𝐴và{1,2,…,𝑛}⊂𝑁.ta nói rằng 𝐴 có 𝑛 phần tử.

Trường hợp2:thủ tục không bao giờ dừng.Ta nói 𝐴 có vô số phần tử hay 𝐴 là một tập hợp vô hạn.

Từ nhận xét trên ta có

Định nghĩa 2.3.1:

i. Một tập hợp 𝐴 được nói là hữu hạn và có 𝑛 phần tử nếu tồn tại một song ánh giữa 𝐴 và tập hợp con { 1,2,…, 𝑛} của 𝑁. Ta viết |𝐴| = 𝑛.

ii. Nếu 𝐴 không hữu hạn, ta nói 𝐴 vô hạn

Chú ý:

1. Do nhận xét trên, phép toán chỉ ra cho ta một thuật toán cụ thể để xây dựng một song ánh giữa 𝐴 và { 1,2,…, 𝑛} nếu 𝐴 hữu hạn, trong khi Định nghĩa 2.3.1 chỉ đòi hỏi tồn tại một song ánh như vậy.

2. Hai tập hợp hữu hạn 𝐴, 𝐵 có cùng số phần tử sẽ tương ứng 1 - 1 với nhau, nghĩa là tồn tại một song ánh 𝐴 ⟷ 𝐵. Ta cũng nói 𝐴 và 𝐵 có cùng lực lượng. Tổng quát hơn ta có

Định nghĩa 2.3.2:

i. Một tập hợp 𝐴 được nói là có lực lượng bé hơn lực lượng của 𝐵 nếu tồn tại một đơn ánh từ 𝐴 vào 𝐵.

ii. Hai tập hợp 𝐴 và 𝐵 được nói là đồng lực lượng nếu có một song ánh 𝐴 ⟷ 𝐵

Chú ý:  Giả sử tồn tại một đơn ánh ƒ từ 𝐴 vào 𝐵. Đặt 𝐶 = ƒ( 𝐴) và là phần bù của 𝐶̅ trong 𝐵. Chọn một phần tử 𝑎 ∈ 𝐴 tùy ý. Ta sẽ định nghĩa một ánh xạ 𝑔: 𝐵 ⟶ 𝐴 như sau:

• Nếu 𝑦 ∈ 𝐶 thì tồn tại duy nhất 𝑥 ∈ 𝐴 sao cho 𝑦 = ƒ( 𝑥) . Ta đặt 𝑔( 𝑦) = 𝑥
• Nếu 𝑦 ∈ 𝐶̅, ta đặt 𝑔( 𝑦) = 𝑎

Khi ấy rõ ràng 𝑔 là một ánh xạ từ 𝐵 vào 𝐴 sao cho 𝑔( 𝐶) = 𝐴. Suy ra 𝑔 là toàn ánh.

Ngược lại giả sử tồn tại một toàn ánh 𝑔: 𝐵 ⟶ 𝐴. Khi ấy với 𝑥 ∈ 𝐴 tùy ý, 𝑔−1( 𝑥) là một tập con khác ∅ nên ta có thể chọn một phần tử nhất định 𝑦 ∈ 𝑔−1( 𝑥) . Đặt ƒ( 𝑥) = 𝑦, ta sẽ được một ánh xạ ƒ từ 𝐴 vào 𝐵. Do cách xây dựng với 𝑥 ≠ 𝑥’ thì 𝑔−1( 𝑥) ∩ 𝑔−1( 𝑥′) = ∅ nên ƒ( 𝑥) = ƒ( 𝑥′) , nghĩa là ƒ là đơn ánh. Ở đây ta sử dụng khái niệm chọn 𝑦 ∈ 𝑔−1( 𝑥) một cách trực quan. Theo lý thuyết tập hợp tiên đề thì việc chọn như vậy không hiển nhiên mà được dựa trên Tiên đề chọn. Đương nhiên đối với các tập hợp hữu hạn Tiên đề chọn là không cần thiết. Tóm lại ta đã chứng minh được.

Mệnh đề 2.3.1:

Lực lượng của 𝐴 nhỏ hơn lực lượng của 𝐵 khi và chỉ khi tồn tại một tồn ánh từ 𝐵 lên 𝐴.

Một vấn đề thứ hai là nếu lực lượng của 𝐴 nhỏ hơn lực lượng của 𝐵 và lực lượng của

𝐵 nhỏ hơn lực lượng của 𝐴 thì liệu 𝐴 và 𝐵 có đồng lực lượng không. Khẳng định này được chứng minh trong trường hợp tổng quát, nhưng chứng minh này ra khỏi khuôn khổ của giáo trình Toán Rời rạc.

Tuy nhiên nếu A và B hữu hạn ta có

Định lý 2.3.2:

Giả sử 𝐴 và 𝐵 là hai tập hợp hữu hạn. Nếu tồn tại một đơn ánh từ 𝐴 vào 𝐵 và một đơn ánh từ 𝐵 vào 𝐴 thì 𝐴 và 𝐵 có cùng số phần tử. Hơn nữa mọi đơn ánh (tương ứng với toàn ánh) từ 𝐴 vào (tương ứng lên) 𝐵 là một song ánh.

Chứng minh: Gọi ƒ là một đơn ánh tùy ý từ 𝐴 vào 𝐵

Đặt 𝐶 = ƒ( 𝐴) và 𝐶 là phần bù của 𝐶 trong 𝐵 thì Mệnh đề 2.3.3 dưới đây cho:

|𝐵| = |𝐶| + |𝐶̅|

Do f rõ ràng xác định một song ánh giữa 𝐴 và 𝐶 nên ta có

|𝐵| = |𝐴| + |𝐶̅| ≥ |𝐴|

Tương tự nếu tồn tại một đơn ánh từ 𝐵 vào 𝐴 ta sẽ có

|𝐴| ≥ |𝐵|

Suy ra

|𝐴| = |𝐵|

Đặc biệt

|𝐶̅| = 0

Giả sử g là một toàn ánh từ 𝐵 lên 𝐴. Trên đây ta dang xây dựng một đơn ánh ƒ từ 𝐴 vào 𝐵 sao cho ƒ( 𝑥) ∈ 𝑔−1( 𝑥)  với mọi 𝑥 ∈ 𝐴. Theo chứng minh trên ƒ  là song ánh  nên rõ ràng 𝑔 cũng là song ánh.

Mệnh đề 2.3.3 (Nguyên lý cộng):

Giả sử 𝐵  là  một  tập  hợp  con  của  tập  hợp  hữu  hạn 𝐴.  Gọi 𝐵̅  là  phần  bù  của 𝐵  trong 𝐴. Khi ấy ta có:

|𝐴| =  |𝐵| +  | 𝐵̅|

Chứng  minh:  Gọi 𝑚, 𝑛 là số phần tử của 𝐵 và 𝐵̅  tương ứng. Khi ấy tồn  tại  một song ánh ƒ từ 𝐵 lên { 1,2,…, 𝑚}  và  một song  ánh 𝑔  từ 𝐵̅  lên { 1,2,…, 𝑛}. Ta định  nghĩa ánh xạ ℎ  từ 𝐴 vào { 1,2,…, 𝑚 +  𝑛} như sau:

• Nếu 𝑥 ∈ 𝐵 ta đặt ℎ( 𝑥) = ƒ( 𝑥)
• Nếu 𝑥 ∈ 𝐵̅  ta đặt ℎ( 𝑥)  =  𝑔( 𝑥) +  𝑚

Rõ ràng ℎ là một song ánh nên |𝐴| = 𝑚 + 𝑛                         

Ví dụ: Để chuẩn bị vào giai đoạn 2, có 150 sinh viên chương trình 1 đã ghi tên học môn Toán Rời rạc và 120 sinh viên ghi tên học Vi tích phân 3 ở học kỳ này. Hỏi có bao nhiêu sinh viên ghi tên học một trong hai môn biết rằng không có sinh viên nào học cả hai môn.

Gọi 𝐴 là tập hợp các sinh viên ghi tên học môn Toán rời rạc và 𝐵 là tập hợp sinh viên ghi tên học Vi tích phân 3. Khi ấy tập hợp các sinh viên ghi tên học một trong hai môn là

𝐴 𝖴 𝐵 và 𝐵 chính là phần bù của 𝐴 trong 𝐴 𝖴 𝐵 nên ta có

|𝐴 𝖴 𝐵| = |𝐴| + |𝐵| = 150 + 120 = 270

Qua ví dụ trên, ta thấy quá trình đếm các sinh viên học một trong hai môn có thể được thực hiện bằng hai cách: đếm các sinh viên học Toán rời rạc và đếm các sinh viên học Vi tích phân 3. Hai cách này là loại trừ lẫn nhau theo nghĩa chúng không thể đồng thời xảy ra. Khi ấy ta cũng có thể phát biểu lại Mệnh đề 2.3.3 dưới dạng:

Nguyên lý cộng: Nếu một quá trình có thể được thực hiện bằng một trong hai cách loại trừ lẫn nhau: cách thứ nhất cho 𝑚 kết quả và cách thứ hai cho 𝑛 kết quả. Khi ấy việc thực hiện quá trình cho 𝑚 + 𝑛 kết quả.

Chú ý:

1. Trong ví dụ trên nếu có một số sinh viên ghi tên học cả hai môn, chẳng hạn như 50 thì tập hợp 𝐴 ∩ 𝐵 ≠ ∅ và có 50 phần tử. Trong trường hợp này |𝐴| +  |𝐵| không phải là số phần tử của |𝐴 𝖴 𝐵| vì |𝐴 ∩ 𝐵| được tính hai lần trong |𝐴| và |𝐵|. Do đó ta có dạng mở rộng của nguyên lý cộng là:

|𝐴 𝖴 𝐵| =  |𝐴| + |𝐵| − |𝐴 ∩ 𝐵| = 150 + 120 − 50 = 220     (2.3.1)

2. Mệnh đề 2.3.3 cũng có thể được mở rộng theo hướng có nhiều hơn 2 tập hợp. Giả sử có n tập hợp: 𝐶₁, 𝐶₂,…, 𝐶_𝑛.Ta nói các tập hợp này đôi một rời nhau nếu 𝐶_i ∩ 𝐶_j = ∅ nếu i ≠ j. Ta có

Mệnh đề 2.3.4 (Nguyên lý cộng mở rộng):

Nếu tập hợp hữu hạn 𝐶 có thể viết như là hợp các tập hợp 𝐶1, 𝐶2,…, 𝐶𝑛 đôi một rời nhau thì

|𝐶| = |𝐶1| + |𝐶2| + ⋯ + |𝐶𝑛|

Chứng minh: Sử dụng Mệnh đề 2.3.3 và Nguyên lý quy nạp trên 𝑛

Ngoài nguyên lý cộng, một công cụ đếm hữu hiệu là:

Nguyên lý nhân: Nếu một quá trình có thể thực hiện theo hai đoạn liên tiếp độc lập với nhau sao cho có 𝑚 cách khác nhau để thực hiện giai đoạn 1 và với mỗi cách lựa chọn trong giai đoạn 1 đều có 𝑛 cách khác nhau để thực hiên giai đoạn 2. Khi ấy có 𝑚𝑛 cách khác nhau để thực hiên toàn bộ quá trình.

Chú ý: nói rằng hai giai đoạn được thực hiện độc lập được thực hiện ( 𝑎, 𝑏) và ( 𝑐, 𝑑) sẽ cho hai kết quả khác nhau nếu một trong hai trường hợp sau xảy ra:

• Hai cách thực hiên giai đoạn 1 khác nhau 𝑎 ≠ 𝑐
• 𝑎 = 𝑐 và hai cách thực hiện giai đoạn 2 khác nhau 𝑏 ≠ 𝑑

Ví dụ: Để chuẩn bị mở một văn phòng đại diện ở nước ngoài, Giám đốc của Công ty X cần nghe lời cố vấn về pháp luật từ một luật sư chọn trong số 5 luật sư và cố vấn về địa ốc từ một chuyên viên địa ốc chọn trong số 3 chuyên viên địa ốc. Do đó theo Nguyên lý nhân có tất cả 5x3=15 phương án để Giám đốc Công ty X tiếp xúc với hai chuyên viên trong hai lĩnh vực trên.

Trong ví dụ trên, gọi 𝐴 là tập hợp các luật sư và 𝐵 là tập hợp các chuyên viên địa ốc cần tham khảo. Khi ấy một phương án tham khảo cố vấn là một cặp có thứ tự ( 𝑎, 𝑏) với 𝑎 ∈ 𝐴, 𝑏 ∈ 𝐵. Tập hợp các phương án tham khảo cố vấn chính là t ích Descartes 𝐴 × 𝐵 theo định nghĩa dưới đây.

Định nghĩa 2.3.3:

Tích Descartes của 2 tập hợp 𝐴, 𝐵 ký hiệu bởi 𝐴 × 𝐵 cũng là một tập hợp hữu hạn vả ta có:

|𝐴 × 𝐵| = | 𝐴| |𝐵|

Chứng minh: Quá trình đếm các phần tử của 𝐴 × 𝐵 được thực hiên theo hai giai đoạn: có |𝐴|cách khác nhau để chọn 1 phần tử tùy ý của 𝐴 với mỗi cách chọn phần tử 𝑎 ∈ 𝐴, có |𝐵| cách chọn một phần tử tùy ý 𝑏 ∈ 𝐵 để tạo thành các cặp khác nhau ( 𝑎, 𝑏) . Do đó theo nguyên lý nhân có |𝐴| |𝐵| cách chọn các cặp ( 𝑎, 𝑏) khác nhau. Nói cách khác

|𝐴 × 𝐵| = |𝐴| |𝐵|

Để xây dựng một song ánh cụ thể từ 𝐴 × 𝐵 lên { 1,2,…, 𝑚𝑛}, trong đó 𝑚 = |𝐴| , 𝑛 = |𝐵| ta làm như sau:

Xét các song ánh

ƒ: 𝐴 ⟷ { 1,2,…, 𝑚}

và 𝑔: 𝐵 ⟷ { 1,2,…, 𝑛}

Ta định nghĩa ánh xạ ℎ: 𝐴 × 𝐵 ⟶ { 1,2,…, 𝑚𝑛} như sau:

ℎ( 𝑎, 𝑏) = ( 𝑔( 𝑏) − 1) × 𝑚 + ƒ( 𝑎)

Giả sử

ℎ( 𝑎, 𝑏) = ℎ( 𝑎′, 𝑏′)

Khi ấy

(𝑔(𝑏) − 1) 𝑚 + ƒ( 𝑎) =  ( 𝑔( 𝑏′) − 1) 𝑚 + ƒ( 𝑎′)  (2.3.2)             

Ta có thể giả sử ƒ( 𝑎′) ≤ ƒ( 𝑎) . Do (2.3.2) ta có:

ƒ( 𝑎) − ƒ( 𝑎′) =  (𝑔( 𝑏′) − 𝑔( 𝑏) )𝑚

Nhưng 0 ≤ ƒ( 𝑎) − ƒ( 𝑎′) <  𝑚 và (𝑔( 𝑏′) − 𝑔( 𝑏) )𝑚 ≥ 𝑚 nếu 𝑔( 𝑏′) − 𝑔( 𝑏) > 0

Suy ra ƒ( 𝑎) = ƒ( 𝑎′) và 𝑔( 𝑏′) − 𝑔( 𝑏)

Do đó ( 𝑎, 𝑏) = ( 𝑎′, 𝑏′) vì ƒ và 𝑔 là song ánh

Sau cùng giả sử 𝑘 là một số nguyên bất kỳ sao cho 1 ≤ 𝑘 ≤ 𝑚𝑛. Gọi i là một số nguyên tự nhiên lớn nhất sao cho 𝑚i < 𝑘. Khi ấy

𝑚i < 𝑘 ≤ 𝑚( i + 1)

Nên

1 ≤ j = 𝑘 − 𝑚i ≤ 𝑚

Và

0 ≤ i ≤ $\frac{mn}{m}$ = n

Đặt 𝑎 = ƒ⁻¹( j) và 𝑏 =  𝑔⁻¹( i + 1)

Rõ ràng  ℎ( 𝑎, 𝑏)  = ( 𝑔𝑔⁻¹( i + 1) − 1) 𝑚 + ƒƒ⁻¹( j) =   i𝑚 + j = 𝑘

Chú ý: ƒ⁻¹ và 𝑔⁻¹ cho phép viết 𝐴 và 𝐵 dưới dạng

𝐴 = { 𝑎₁, 𝑎₂,…, 𝑎_𝑚} và 𝐵 =  { 𝑏₁, 𝑏₂,…, 𝑏_𝑛}

Ta nói các phần tử của 𝐴 (tương ứng 𝐵) đã được đánh chỉ số bởi ƒ⁻¹ (tương ứng ƒ⁻¹). Khi ấy ánh xạ ℎ có thể viết: ℎ(𝑎_i, 𝑏_j) = ( j − 1) 𝑚 + i

Nói cách khác ta đã “đếm” các phần tử của 𝐴 × 𝐵 theo 𝑛 mảng đặt kế tiếp nhau: {( 𝑎₁, 𝑏₁), ( 𝑎₂, 𝑏₁) ,…,( 𝑎_𝑚, 𝑏₁) }, {( 𝑎₁, 𝑏₂) , ( 𝑎₂, 𝑏₂),…𝑎_𝑚,𝑏₂}…, {( 𝑎₁, 𝑏_𝑛) , ( 𝑎₂, 𝑏_𝑛) ,…,( 𝑎_𝑚, 𝑏_𝑛) }

Gọi các mảng này lần lượt là 𝐶₁, 𝐶₂,…, 𝐶_𝑛 thì chúng đều tương ứng 1 – 1 với 𝐴 nên có cùng số phần tử là 𝑚. Hơn nữa các tập hợp này đôi một rời nhau nên ảnh của ℎ có 𝑚 × 𝑛 phần tử và do đó ℎ là song ánh.

Nguyên lý nhân có thể được mở rộng cho quá trình nhiều hơn hai giai đoạn. Tương tự Định nghĩa 2.3.3 và Định nghĩa 2.3.5 có thể được mở rộng cho tích Descartes của nhiều hơn hai tập hợp.

Định nghĩa 2.3.4:

Có 𝑛 tập hợp không rỗng 𝐴₁, 𝐴₂,…, 𝐴_𝑛

Một bộ 𝑛 phần tử là một họ phần tử có dạng ( 𝑎₁, 𝑎₂,…, 𝑎_𝑛), với  𝑎₁ ∈ 𝐴₁, 𝑎₂ ∈ 𝐴₂,…, 𝑎_𝑛 ∈ 𝐴_𝑛 hai bộ 𝑛( 𝑎1, 𝑎2,…, 𝑎𝑛) ,( 𝑎′1, 𝑎′ ,…, 𝑎′ ) được nói là bằng nhau nếu 𝑎 = 𝑎′ , 𝑎 =  𝑎′ ,…, 𝑎 = 𝑎′

Tập hợp tất cả các bộ n phần tử được gọi là tích Descartes của 𝐴₁, 𝐴₂,…, 𝐴_𝑛 và ký hiệu bởi 𝐴₁ × 𝐴₂ × …× 𝐴_𝑛

𝐴₁ × 𝐴₂ × …× 𝐴_𝑛 = {( 𝑎₁, 𝑎₂,…, 𝑎_𝑛)/ 𝑎₁ ∈ 𝐴₁, 𝑎₂ ∈ 𝐴₂,…, 𝑎_𝑛 ∈ 𝐴_𝑛}

Định lý 2 .3.6 :

Nếu A₁,A₂,…,A_n hữu hạn thì $\underset{i=1}{\overset{n}{G}}$ 𝐴i cũng hữu hạn và ta có

|$\underset{i=1}{\overset{n}{G}}$ 𝐴_i|     =  |𝐴₁||𝐴₂| …|𝐴_𝑛|

Chứng minh: dùng Định lý 2.3.5 và nguyên lý quy nạp

Ví dụ: Sinh viên Giai đoạn 1 thuộc Chương trình 1 của Trường Đại học Khoa học Tự nhiên cử ra một Ban Đại diện gồm môt sinh viên Toán – Tin, một sinh viên Công nghệ Thông tin, một sinh viên Vật lý, một sinh viên Hóa học. Hỏi có bao nhiêu cách chọn ra ban Đại diện biết rằng có 300 sinh viên Toán – Tin, 400 sinh viên Công nghệ Thông tin, 200 sinh viên Vật lý và 300 sinh viên Hóa?

Gọi 𝐴1 , 𝐴2, 𝐴3, 𝐴4 lần lượt là tập hợp các sinh viên Giai đoạn 1 của các ngành Toán – Tin, Công nghệ thông tin, Lý, Hóa. Khi ấy một Ban Đại diện chính là một bộ 4:

Do đó theo Định lý 2.3.6 số cách chọn Ban Đại diện là:

$\left|\underset{i=1}{\overset{4}{G{A}_I}}\right|$ = $\underset{i=1}{\overset{4}{G}}\left|A_i\right|$ = $300\times 400\times 200\times 300=7.200.000.000$

GIẢI TÍCH TỔ HỢP

Cho trước hai tập hợp 𝐴 và 𝐵, tập hợp tất cả các ánh xạ từ 𝐴 vào 𝐵 được ký hiệu bởi 𝐵^Æ. Giả sử | 𝐴| = 𝑚, ta có 𝐴 = { 𝑎₁, 𝑎₂,…, 𝑎_𝑚}

Rõ ràng một ánh xạ ƒ từ 𝐴 vào 𝐵 được xác định hoàn toàn bằng cách chọn ra 𝑚 phần tử 𝑏₁ = ƒ( 𝑎₁) , 𝑏₂ = ƒ( 𝑎₂) ,…, 𝑏_𝑚 = ƒ( 𝑎_𝑚)

Nói cách khác ƒ được xác định bởi bộ 𝑚: ( ƒ( 𝑎₁) , ƒ( 𝑎₂) ,…, ƒ( 𝑎_𝑚) ) ∈ 𝐵_𝑚

Như vậy ta được một ánh xạ: 𝜑: 𝐵^Æ ⟶ 𝐵^𝑚

với   𝜑( ƒ) =  ( ƒ( 𝑎₁) , ƒ( 𝑎₂) ,…, ƒ( 𝑎_𝑚) ) ∈ B^m         (2.4.1)

Ngược lại cho trước ( 𝑏1, 𝑏2,…, 𝑏𝑚) ∈ 𝐵𝑚 thì ta định nghĩa được một ánh xạ duy nhất ƒ ∈ 𝐵^Æ bởi:

ƒ( 𝑎₁) =  𝑏₁, ƒ( 𝑎₂) =  𝑏₂,…, ƒ( 𝑎_𝑚) =  𝑏_𝑚

Mệnh đề 2.4.1:

Giả sử |𝐴| = 𝑚 với 𝐴 = { 𝑎₁, 𝑎₂,…, 𝑎_𝑚} thì (2.4.1) xác định một song ánh giữa 𝐵^Æ và 𝐵𝑚. Đặc biệt nếu 𝐵 hữu hạn thì 𝐵Æ cũng hữu hạn và ta có:

|𝐵^Æ| = | 𝐵|^|Æ|

Chú ý: trong phép tương ứng (2.4.1), ƒ là một đơn ánh khi và chỉ khi các phần tử ƒ( 𝑎₁), ƒ( 𝑎₂) ,…, ƒ( 𝑎_𝑚) là đôi một khác nhau. Từ đó ta có một quá trình 𝑚 bước để đếm các đơn ánh từ 𝐴 vào 𝐵.

Bước 1 : Chọn tùy ý một phần tử 𝑏₁ ∈ 𝐵. Ở bước này có 𝑛 cách chọn 𝑏₁

Bước 2: Chọn tùy ý một phần tử 𝑏₂ ∈ 𝐵 khác với 𝑏₁ nghĩa là một phần tử 𝑏₂ ∈ 𝐵\ { 𝑏₁ }.

Ở đây 𝐵\ {𝑏₁ } chỉ phần bù của { 𝑏₁} trong 𝐵. Ta có 𝑛 − 1 cách chọn 𝑏₂

Bước 𝑚: chọn tùy ý một phần tử 𝑏_𝑚 ∈ 𝐵\ { 𝑏₁, 𝑏₂,…, 𝑏_𝑚−1}. Do 𝑛 − ( 𝑚 − 1) = 𝑛 − 𝑚 + 1, nên có 𝑛 − 𝑚 + 1 cách chọn 𝑏_𝑚.

Chú ý rằng để có thể tiến hành đến Bước thứ 𝑚 ta cần có 𝑛 − 𝑚 + 1 ≥ 1, hay 𝑛 ≥ 𝑚.

Do đó áp dụng nguyên lý nhân ta được

Mệnh đề 2.4.2:

Giả sử 𝑚 ≤ 𝑛. Khi ấy số đơn ánh từ 𝐴 vào 𝐵 là:

𝑛( 𝑛 − 1) …( 𝑛 − 𝑚 + 1)

Nếu |𝐴| = |𝐵| = 𝑛 thì ta có

Hệ quả 1 : số song ánh từ 𝐴 lên 𝐵 là :

𝑛( 𝑛 − 1) …1 = 𝑛!

Chứng minh: nếu |𝐴| = |𝐵| thì mọi đơn ánh từ |𝐴| vào | 𝐵| cũng là một song ánh.

Trong trường hợp 𝐴 = 𝐵 thì một song ánh từ 𝐴 lên chính nó còn được gọi là một phép hoán vị của 𝐴. Do đó Hệ quả 1 có thể được phát biểu lại:

Hệ quả 2 : Số các phép hoán vị của một tập hợp có 𝑛 phần tử là 𝑛!

Định nghĩa 2.4.1:

Đặt 𝐵 = { 1,2,…, 𝑛}

• Một chỉnh hợp của 𝑛 phần tử chọn 𝑚 là một phép chọn ra 𝑚 phần tử phân biệt trong 𝐵 theo một thứ tự nào đó
• Một tổ hợp của 𝑛 phần tử chọn 𝑚 là một phép chọn ra 𝑚 phần tử phân biệt trong 𝐵 không kể thứ tự.

Định lý 2.4.1 :

• Số các chỉnh hợp của 𝑛 phần tử chọn 𝑚 là: $A_n^m$ = 𝑛( 𝑛 − 1) …( 𝑛 − 𝑚 + 1)
• Số các chỉnh hợp của 𝑛 phần tử chọn 𝑚 là: $C_n^m$ = 𝑛( 𝑛−1) …( 𝑛−𝑚+1)

Chứng minh:

Với 𝐵 = { 1,2,…, 𝑛} thì một chỉnh hợp của 𝑛 phần tử chọn 𝑚 không gì khác hơn một bộ ( 𝑏₁, 𝑏₂,…, 𝑏𝑚) ∈ 𝐵𝑚 đôi một khác nhau. Do đó số chỉnh hợp được cho bởi Mệnh đề 2.4.2. Ta sẽ tính số tổ hợp bằng cách đếm lại số chỉnh hợp theo một quá trình hai bước:

Bước 1: chọn tùy ý một tổ hợp của 𝑛 phần tử chọn 𝑚, nói cách khác chọn ra một tập hợp con 𝐵’ có m phần tử của 𝐵. Số cách chọn khác nhau chính là số tổ hợp

Bước 2: với một tập hợp con 𝐵’, ta có thể chọn ra m phần tử phân biệt của 𝐵’ theo một thứ tự nhất định: ( 𝑏₁, 𝑏₂,…, 𝑏_𝑚) . Số cách chọn chính là số phép hoán vị của 𝐵’ nên bằng 𝑚!

Bằng hai bước trên ta đã đếm được tất cả các chỉnh hợp của 𝑛 phần tử chọn 𝑚 nên:

$A_n^m=C_n^m\times m!$

Suy ra

$C_n^m=\frac{n(n-1)...(n-m+1)}{m!}$

Chú ý: Ta thường ký hiệu số tổ hợp bởi $\left(\begin{array}{c}n\\ m\end{array}\right)$và gọi là hệ số nhị thức . Hệ số nhị thức có thể đặt dưới dạng đối xứng:

$C_n^m=\left(\begin{array}{c}n\\ m\end{array}\right)=\frac{n(n-1)...(n-m+1)\times (n-m)!}{m!(n-m)!}=\frac{n!}{m!(n-m)!}$

Dưới dạng trên ta thấy ngay:

$\left(\begin{array}{c}n\\ m\end{array}\right)=\left(\begin{array}{c}n\\ n-m\end{array}\right)$

Định lý 2.4.4 :

Với 𝑚 ≤ 𝑛 ta có $\left(\begin{array}{c}n+1\\ m\end{array}\right)=\left(\begin{array}{c}n\\ m\end{array}\right)+\left(\begin{array}{c}n\\ m-1\end{array}\right)$

Chứng minh: Ta sẽ chọn ra các tổ hợp của 𝑛 + 1 phần tử chọn 𝑚 bằng một trong hai cách loại trừ lẫn nhau:

Cách 1: chọn ra một tập hợp con 𝐵’ có m phần tử phân biệt trong { 1,2,…, 𝑛 + 1} không chứa 𝑛 + 1. Rõ ràng 𝐵’ cũng là một tập hợp con m phần tử của { 1,2,…, 𝑛} nên có cách chọn.

Cách 2: chọn ra một tập hợp con 𝐵’’ có m phần tử phân biệt trong { 1,2,…, 𝑛 + 1}. Rõ ràng 𝐵’’\ { 𝑛 + 1} là một tập hợp con 𝑚 − 1 phần tử phân biệt của { 1,2,…, 𝑛} nên có $\left(\begin{array}{c}n\\ m-1\end{array}\right)$ cách chọn

Do đó theo nguyên lý cộng, số tổ hợp của 𝑛 + 1 phần tử chọn 𝑚 thỏa (2.4.2)

Để hiểu rõ tại sao số tổ hợp còn được gọi là hệ số nhị thức, ta hãy chứng minh công thức dưới đây gọi là Công thức nhị thức Newton

${(x+y)}^n=x^n+\left(\begin{array}{c}n\\ 1\end{array}\right) x^{n-1}y+...+\left(\begin{array}{c}n\\ n\end{array}\right) y^n=\sum _{n=0}^n\left(\begin{array}{c}n\\ m\end{array}\right) x^{n-m} y^m$

Chứng minh: Ta hãy khai triển ( 𝑥 + 𝑦) ^𝑛 = ( 𝑥 + 𝑦) ( 𝑥 + 𝑦) …( 𝑥 + 𝑦) thành tổng các số hạng có dạng 𝑎₁𝑎₂ …𝑎_𝑛 trong đó 𝑎_i = 𝑥 hay 𝑎_i = 𝑦, 1 ≤ i ≤ 𝑛. Với 0 ≤ 𝑚 ≤ 𝑛 ta gộp tất cả các số hạng trong đó có đúng 𝑚 thừa số bằng 𝑦. Các số hạng này đều có dạng 𝑥^𝑛−𝑚𝑦^𝑚. Hơn nữa số các số hạng như vậy chính là số cách chọn 𝑚 phần tử phân biệt của { 1,2,…, 𝑛}: trong đó là số tổ hợp nên (2.4.3) được chứng minh.

Chú ý: Theo nguyên lý cộng, vế phải của (2.4.4) chính là số các tập hợp con của { 1,2,…, 𝑛} nên ta đếm được số các tập hợp con của { 1,2,…, 𝑛} chính là 2^𝑛. Thật ra ta có thể đếm gián tiếp số các tập hợp con của một tập hợp 𝐵 có 𝑛 phần tử như sau:

Gọi 𝐴 là một tập hợp con bất kỳ của 𝐵, ta sẽ định nghĩa hàm đặc trưng của 𝐴 bởi:

$3_{AE}\left(x\right) = \left\{\begin{array}{l}1 nếu x\in A\\ 0 nếu x không thộc A\end{array}\right.$

Rõ ràng 3_Æ ∈ { 0,1} ^𝐵. Ngược lại, cho trước ƒ ∈ { 0,1} ^𝐵. Đặt 𝐴 =  ƒ⁻¹( 1). Khi ấy rõ ràng ƒ = 3_Æ. Bằng cách này ta được một song ánh giữa tập hợp 𝑃( 𝐵) gồm tất cả các tập hợp con của 𝐵 và {0,1} ^𝐵. Suy ra |𝑃( 𝐵) | = | {0,1}|^|𝐵| = 2^𝑛

Hai tập hợp 𝑃( 𝐵) và { 0,1} ^ 𝐵 (ký hiệu là 2^𝐵) là các đại số Bool sẽ được xét trong chương 4.

Bây giờ ta hãy mở rộng khái niệm tổ hợp trong đó có phép lặp lại. Trước hết ta hãy xét một ví dụ: một học sinh đến cửa hàng mua 4 cây bút chọn trong 3 màu khác nhau là xanh, đỏ và vàng. Có bao nhiêu cách khác nhau để chọn mua hàng?

Trước hết ta hãy liệt kê các trường hợp khác nhau:

•  4 bút cùng màu: có 3 trường hợp
•  3 bút cùng màu và bút thứ tư chọn tùy ý trong hai màu còn lại: có 3x2=6 trường hợp (Nguyên lý nhân!)
•  2 bút cùng màu và 2 bút kia chọn trong 2 màu còn lại: 3 trường hợp
•  2 cặp bút cùng màu: có  $\left(\begin{array}{c}3\\ 2\end{array}\right)$ = 3 trường hợp

Như vậy tổng cộng có 15 cách mua hàng khác nhau

Tuy nhiên nếu liệt kê như vậy rất khó mở rộng cho trường hợp có nhiều bút và nhiều màu để chọn. Thay vì như vậy, ta sẽ biểu diễn mỗi trường hợp bởi 4 dấu “+” và 2 dấu “−” đặt liên tiếp trên một đường thẳng: số dấu + bên trái dấu – đầu tiên chỉ số bút xanh, số dấu + nằm giữa 2 dấu – chỉ số bút đỏ và số dấu + nằm bên phải dấu – cuối cùng chỉ số bút màu vàng. Như vậy trường hợp mua 4 bút xanh được biểu diễn bởi + + + + − −

Cũng thế trường hợp mua 1 bút xanh và 3 bút vàng được biểu diễn bởi + − − + + +

Như thế mỗi trường hợp tương ứng với việc lựa chọn vị trí của 2 dấu – trong số 6 ký hiệu, nói cách khác ứng với 1 tập hợp con 2 phần tử của tập hợp { 1,2,…,6}

Từ đó suy ra số cách mua hàng khác nhau chính là

 $\left(\begin{array}{c}6\\ 2\end{array}\right)=\frac{6\times 5}{2}=15$ 

Bằng cách này ta có thể tổng quát hóa việc chọn ra 𝑟 vật trong số 𝑛 loại vật khác nhau trong đó mỗi loại vật có thể được chọn lại nhiều lần. như trên mỗi trường hợp lựa chọn có thể được biểu diễn bằng cách chèn ( 𝑛 − 1) dấu – vào trong số 𝑟 dấu + để chia đoạn thẳng thành 𝑛 đoạn tương ứng với số vật mỗi loại. Do đó số cách lựa chọn khác nhau mà ta gọi là số tổ hợp có lặp lại của n vật chọn 𝑟 chính là:

$\left(\begin{array}{c}n+r-1\\ n-1\end{array}\right)=\left(\begin{array}{c}n+r-1\\ r\end{array}\right)$

Áp dụng:

Có 𝑟 vật đồng nhất nhau, hỏi bao nhiêu cách chia chúng vào 𝑛 hộp phân biệt nhau?

Ở đây mỗi cách chia cũng chính là một tổ hợp của 𝑛 vật chọn 𝑟 nên số cách chia khác nhau chính là $\left(\begin{array}{c}n+r-1\\ r\end{array}\right)$

Xét phương trình: 𝑥₁ + 𝑥₂ + ⋯ + 𝑥_𝑛 = r 

Trong đó 𝑛 và 𝑟 là các số nguyên không âm cho trước và 𝑥₁, 𝑥₂,…, 𝑥_𝑛 là các ẩn lấy giá trị nguyên không âm. Ta hãy tìm xem phương trình trên có bao nhiêu lời giải với một cách chia 𝑟 vật đồng nhất nhau vào n hộp phân biệt: 𝑥_i chính là số vật chứa trong hộp thứ i.

Do đó số lời giải chính là số tổ hợp có lặp của 𝑛 vật chọn 𝑟: $\left(\begin{array}{c}n+r-1\\ r\end{array}\right)$

NGUYÊN LÝ CHUỒNG BỒ CÂU

Trong Mệnh đề 2.4.1, ta đã giả sử |𝐴| = 𝑚 ≤ |𝐵| = 𝑛 để có thể chọn ra được một họ 𝑚 phần tử phân biệt có thứ tự của 𝐵; nói cách khác để chọn ra được một đơn ánh từ 𝐴 vào 𝐵. Trong trường hợp 𝑚 > 𝑛 thì không tồn tại đơn ánh từ 𝐴 vào 𝐵 theo nguyên lý chuồng Bồ câu sau đây

Nguyên lý chuồng Bồ câu: nếu chuồng bồ câu có ít cửa (pigeon hole) hơn số bồ câu thì ít nhất hai chim bồ câu ở chung trong một cửa.

Ví dụ:

1. Trong ví dụ trên, 𝐴 là số bồ câu và 𝐵 là số cửa. Một ánh xạ ƒ: 𝐴 ⟶ 𝐵 chính là một cách xếp chim bồ câu vào các cửa. Nói rằng có 2 chim bồ câu ở chung một cửa có nghĩa là có 2 phần tử phân biệt của 𝐴 có chung ảnh nên ƒ không đơn ánh.

2. Trong một nhóm có 367 người sẽ có ít nhất hai người có cùng ngày tháng sinh. Ở đây số các ngày tháng sinh khác nhau (366 ngày, kể cả ngày 29 tháng 02) chính là số cửa của chuồng bồ câu.