CHƯƠNG 3: QUAN HỆ
QUAN HỆ
Định nghĩa 3.1.1
Một quan hệ giữa tập hợp ? và tập hợp ? là một tập hợp con ? của ? × ?. Nếu ( ?, ?) ∈ ?, ta viết ???.
Một quan hệ giữa ? và ? được gọi là quan hệ trên ?
Ví dụ:
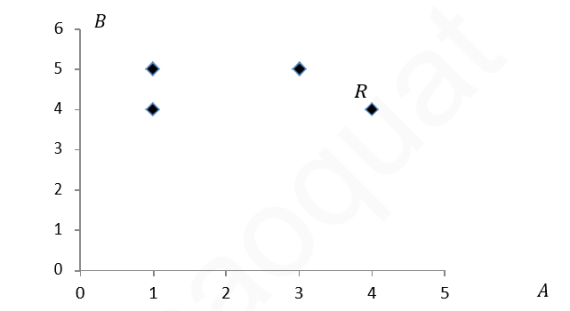
1. ? = { 1,2,3,4}, ? = { 4,5}
? = {( 1,4),( 1,5),( 3,5),( 4,4)}
Là một quan hệ giữa ? và ?. Ta thường biểu diễn quan hệ ? bởi sơ đồ sau:
2. Quan hệ “=” trên một tập hợp ? bất kỳ: ( ???) ⟺ ? = ?
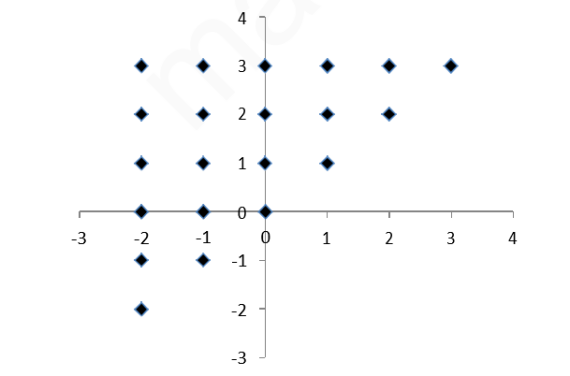
3. Quan hệ “≤” trên ?, O hay ?: ( ???) ⟺ ? ≤ ?
Trên ? quan hệ ≤ có thể biểu diễn bởi sơ đồ:
4. Gọi ? là tập hợp các đường thẳng trong mặt phẳng. Quan hệ song song được định nghĩa bởi: ??? ⟺ ?/ / ?
5. Một số nguyên ? được nói là chia hết cho số nguyên ? nếu tồn tại số nguyên ? sao cho ? = ??.
Khi ấy ta cũng nói ? là ước số của ? và ? là bội số của ?.
Giả sử ? là một số nguyên >1 và ? ∈ ?
Xét các bội số không âm của n: 0, ?, 2?,…, ??,…
Trong số này, các bội số ≤ ? tạo thành một tập hợp hữu hạn nên ta có thể tìm được bội số ?? lớn nhất:
?? ≤ ? < ( ? + 1) ?
Đặt ? = ? = ?? ta có ? = ?? + ? ?ới 0 ≤ ? < ?
Ta nói rằng ? và ? là thương số và dư số trong phép chia (có dư) ? cho ?.
Chú ý rằng ? và ? tồn tại duy nhất. thật vậy,giả sử tồn tại ?′, ?′ ∈ ? sao cho:
? = ?′? + ?′, 0 ≤ ? < ?
Ta có thể giả sử ? ≤ ?. Khi ấy: ?? + ? = ?′? + ?′
Suy ra ( ? − ?′) ? = ?′ − ? ≥ 0
Rõ ràng ?′ − ? < ? ≤ ( ? − ?′) ? nếu ? − ?′ ≥ 1
Cho trước số nguyên ? > 1, ta định nghĩa quan hệ: ??? ⟺ ? − ? chia hết cho ? Quan hệ này được nói là quan hệ đồng dư modulo ?. Nếu ??? ta viết: ? ≡ ?( ?o? ?) Rõ ràng khi ấy ? và ? có cùng dư số khi chia cho ?
Với ? = 7 ta có 9 ≡ 2( ?o? 7) và 3 ≡ 10( ?o? 7) nhưng 3 ≢ 6( ?o? 7).
Định nghĩa 3.1.2:
Cho trước các tập hợp ?1, ?2,…, ??. Khi ấy ánh xạ chiếu lên thành phần thứ i là ánh xạ:
?i: ?1 × ?2 × …× ?? ⟼ ?i; ( ?1, ?2,…, ??) ⟼ ?i
1. Ánh xạ chiếu ?i rõ ràng là một toàn ánh
2. Đặc biệt các ánh xạ chiếu ?Æ, ?? từ ? × ? lên ? và ? tương ứng là các toàn ánh. Tuy nhiên nếu ? là tập hợp con của ? × ?, nghĩa là một quan hệ giữa A và B thì ?Æ( ?) và ??( ?) có thể là tập hợp con thực sự của A và B tương ứng như các ví dụ sau cho thấy.
Ví dụ:
1. ? = ? = ?, ? = {( ?, ?) / ? = |?|}
Quan hệ ? được biểu diễn bởi sơ đồ
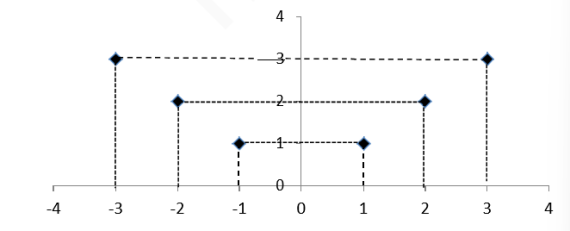
Ta có ??( ?) = ?
Tuy nhiên ??( ?) = ? ? = ?
2. ? = ? = ?, ? = {( ?, ?) ∈ ? × ?/ ? = ?2}
Rõ ràng ??( ?) = ? = ? trong khi ??( ?) = [ 0, + ∞) = {? ∈ ?/ ? ≥ 0} ?
3. ? = ? = [ −1,1] = { ? ∈ ?/ −1 ≤ ? ≤ 1} và ? = {( ?, ?) ∈ ? × ?/ ?2 + ?2 ≤ 1}
Khi ấy ?Æ( ?) = ??( ?) = ? = ? mặc dù ?? × ?
Định nghĩa 3.1.3
Một quan hệ trên các tập hợp ?1 × ?2 × …× ?? là một tập hợp con của
?i = ?1 × ?2 × …× ??
Chú ý:
1. Giả sử ? là một quan hệ trên ?1, ?2,…, ??. Khi ấy các phần tử của ? là những bộ ? ( ?1, ?2,…??)
2. Xét ? số nguyên 1 ≤ i1 < i2 < ⋯ < i? ≤ ?. Khi ấy ta cũng có thể định nghĩa một ánh xạ chiếu
?i1,i2,…,i?: ?1 × ?2 × …× ?? ⟶ ?i1 × ?i2 × …× ?i?
( ?1, ?2,…, ??) ⟼ (?i1, ?i2 ,…, ?i? )
Rõ ràng ?i1,i2,…,i? cũng là một toàn ánh.
Định nghĩa 3.1.4
Nếu ? một quan hệ trên ?1, ?2,…, ?? thì ?i1,i2,…,i? ( ?) được gọi là quan hệ chiếu của ?.
Chú ý:
1. Quan hệ chiếu ?i1,i2,…,i? ( ?) là một quan hệ trên ?i1 × ?i2 × …× ?i?.
2. Trong Lý thuyết về cơ sở dữ liệu mô hình quan hệ, các tập hợp ?1, ?2,…, ?? được gọi là các thuộc tính. Như thế quan hệ chiếu ?i ,i ,…,i? ( ?) chính là quan hệ ban đầu nhưng các thuộc tính không thuộc các tập hợp ?i1, ?i2 ,…, ?i? đã được bỏ qua như ví dụ sau cho thấy
Ví dụ: trong cơ sở dữ liệu Môn học ở Đại học Khoa học Tự nhiên, ta có các tập hợp thuộc tính sau:
?1: các mã số môn học
?2: các tên môn học
?3: các Giảng viên
Quan hệ Môn học - Giảng viên được cho bởi bảng sau:
|
Mã Môn học
|
Tên môn học
|
Giảng viên
|
|
T001
|
Vi tích phân
|
Ông Bình
|
|
T011
|
Toán Rời rạc
|
Ông An
|
|
T012
|
Đại số tuyến tính
|
Ông Minh
|
|
TH001
|
Tin học ĐC A1
|
Cô Hà
|
|
TH002
|
Tin học ĐC A2
|
Cô Hà
|
Quan hệ chiếu ?1 2 (Môn học-Giảng viên) là quan hệ Môn học được cho bởi bảng
|
Mã Môn học
|
Tên Môn học
|
|
T001
|
Vi tích phân
|
|
T011
|
Toán Rời rạc
|
|
T012
|
Đại số tuyến tính
|
|
TH001
|
Tin học ĐC A1
|
|
TH002
|
Tin học ĐC A2
|
Mặt khác quan hệ chiếu ?3 (Môn học – Giảng viên) chính là quan hệ Giảng viên: {Ông Bình, Ông An, Ông Minh, Cô Hà}.
QUAN HỆ TƯƠNG ĐƯƠNG
Định nghĩa 3.2.1
Một quan hệ ? trên tập hợp ? được nói là phản xạ nếu: ∀? ∈ ?, ???
Ví dụ:
1. Quan hệ “=” trên một tập hợp bất kỳ, quan hệ “≤” trên ?, O, ?, quan hệ đống dư trên Z là phản xạ
2. Quan hệ “// ” trên ? là phản xạ. Tuy nhiên quan hệ “⊥” (vuông góc) trên ? không phải là quan hệ phản xạ.
Chú ý: gọi ∆Ælà đường chéo chính của ? × ? : ∆Æ= {( ?, ?) / ? ∈ ?}. Khi ấy quan hệ ? trên ? là phản xạ khi và chỉ khi ? ⊃ ∆Æ.
Định nghĩa 3.2.2
Quan hệ ? trên ? được nói là đối xứng nếu: ∀?, ? ∈ ?, ??? ⟹ ???
Ví dụ:
1. Các quan hệ “= , ≡, //, ⊥” là những quan hệ đối xứng
2. Quan hệ “≤” trên ?, O, ? không phải là quan hệ đối xứng
3. Quan hệ ? = {( 1,2).( 2,1),( 1,3),( 3,1)} trên ? = { 1,2,3,4} là một quan hệ đối xứng nhưng không phản xạ:
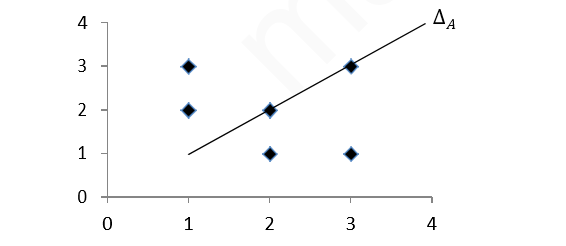
Chú ý: trong hình vẽ trên ta thấy tập hợp ? tự đối xứng qua đường chéo ∆Æ. Tổng quát hơn một quan hệ ? trên tập hợp ? bất kỳ là đối xứng khi và chỉ khi ? là tự đối xứng qua ∆?
Định nghĩa 3.2.3
Một quan hệ ? trên ? được nói là bắc cầu nếu:
∀?, ?, ?, ( ???) ? ( ???) ⟹ ???
Ví dụ:
- Các quan hệ “= , ≡, //, ≤” là các quan hệ bắc cầu
- Quan hệ “⊥” trên ? không phải là quan hệ bắc cầu
- Quan hệ {(1,1),(2,3),(3,4),(2,4)} trên ? = { 1,2,3,4} là bắc cầu
Định nghĩa 3.2.4
Một quan hệ ? trên tập ? được gọi là quan hệ tương đương nếu nó phản xạ, đối xứng, bắc cầu.
Ví dụ:
1. Các quan hệ “= , ≡, //” là các quan hệ tương đương
2. Quan hệ “≤, ⊥” không phải là một quan hệ tương đương
3. Quan hệ ? = {( 1,1),( 2,2),( 3,3),( 2,3),( 3,2)} trên ? = {1,2,3} là quan hệ tương đương
4. Quan hệ “tương đương logic” trên tập hợp các mệnh đề là một quan hệ tương đương.
5. Cho trước một ánh xạ ƒ: ? ⟶ ?. Ta định nghĩa quan hệ ? trên ? như sau:
??? ⟺ ƒ( ?) = ƒ( ?)
Khi đó ? là một quan hệ tương đương.
Định nghĩa 3.2.5
Giả sử ? là một quan hệ tương đương trên ? và ? ∈ ?. Khi ấy lớp tương đương chứa ? là tập hợp con: { ? ∈ ?/ ???}
Chú ý: lớp tương đương chứa ? thường được ký hiệu bởi ?̅ hay [ ?]
Ví dụ: Quan hệ ≡ ( ?o? 3) có ba lớp tương đương:
= {,…, −6, −3,0,3,…}
= {,…, −5, −2,1,4,…}
= {,…, −4, −1,2,5,…}
Để ý rằng:
Như thế { } là một phân hoạch của ?, nghĩa là Z là hợp của 3 tập hợp đôi một rời nhau { 0̅, 1̅, 2̅}. Tỗng quát hơn ta có: Định nghĩa 3.2.1
Giả sử ? là một quan hệ tương đương trên ?. Khi ấy:
i. ∀? ∈ ?, ? ∈ ?̅
ii. ∀?, ? ∈ ?, ??? ⟺
iii. Hai lớp tương đương ?̅ và ?̅ sao cho ?̅ ∩ ?̅ ≠ ∅ thì trùng nhau
Chứng minh:
i. Do tính phản xạ, ???. Nói cách khác ? ∈ ?̅
ii. Giả sử ???. Gọi ? là một phần tử bất kỳ của ?̅
Ta có: ??? và ??? nên ??? do tính bắt cầu.Như thế ?̅ ⊂ ?̅. Mặt khác do tính đối xứng ta cũng có ???. Do đó chứng minh tương tự như trên ta có ?̅ ⊂ ?̅.
Ngược lại giả sử ?̅ = ?̅, do ? ∈ ?̅ nên ? ∈ ?̅. Điều này có nghĩa là ???
iii. Giả sử ?̅ ∩ ?̅ ≠ ∅. Khi ấy tồn tại ? ∈ ?̅ ∩ ?̅, nghĩa là ??? và ???. Do ii) ta có ?̅ = ?̅ = ?̅
Ví dụ:
1. Xét quan hệ ? trên ?: ??? ⟺ ?2 = ?2
Theo ví dụ 5 sau Định nghĩa 3.2.4, ? là quan hệ tương đương xác định bởi ánh xạ
? ⟼ ?2 từ ? vào ?. Các lớp tương đương là { 0},{ −1,1},{ −2,2},…,{ −?, ?},…
Ở đây ? được phân hoạch thành vô số tập hợp con hữu hạn.
Với ? ∈ ?, quan hệ đồng dư (mod ?) là một quan hệ tương đương với ? lớp tương đương 0̅, 1̅, …, ?̅ ̅−̅ ̅1̅. Ta ký hiệu: ?? = { 0̅, 1̅, …, ?̅ ̅−̅ ̅1̅}
Các phần tử của, được gọi là các số nguyên đồng dư mod ?.
Với ?̅, ?̅ ∈ ??, chọn tùy ý ? ∈ ?̅ và ? ∈ ?̅. Ta có thể kiểm tra được ̅?̅+̅ ̅?̅ không phụ thuộc vào ? và ? mà chỉ phụ thuộc vào ?̅ và ?̅. Do đó ta có thể dùng ̅?̅+̅ ̅?̅ để định nghĩa
?̅ + ?̅. Đặc biệt ta có thể chọn ? = ? và ? = ?: ?̅ + ?̅ = ̅?̅+̅ ̅?̅
Tương tự ta có:
Bây giờ ta có thẻ kiểm được 2 phép toán ∙, + trên ?? thỏa các tính chất tương tự như các phép toán ∙, + trên ?:
?̅ + ?̅ = ?̅ + ?̅ và ?̅?̅ = ?̅?̅
- Tính kết hợp: ∀?̅, ?̅, ?,̅
= ( ?̅ + ?̅) + ?̅ và ?̅( ?̅? = ( ?̅?̅) ?
- Tính phân bố: ∀?̅, ?̅, ?̅, ?̅( ?̅ + ?̅) = ?̅?̅ + ?̅?̅
- Phần tử trung hòa: ∀?̅
?̅ + 0̅ = ?̅
?̅1̅ = ?̅
- Phần tử đối: ∀?̅, ?̅ + (̅?̅ ̅−̅ ̅?̅)̅ = 0̅
Ta nói ?? cũng như ? là những vành giao hoán có đơn vị
THỨ TỰ
Định nghĩa 3.3.1
Một quan hệ ? trên tập hợp ? được gọi là phản xứng nếu:
∀?, ?, ( ???) ? ( ???) ⟹ ? = ?
Ví dụ:
Quan hệ “≤” trên ?, O hay R là phản xứng Quan hệ “ ≡,/ / ” không phản xứng
Chú ý: trái với các quan hệ đối xứng, đối với một quan hệ phản xứng ?, mọi bộ phận tự đối xứng của ? đều nằm trong đường chéo ∆Æ
Định nghĩa 3.3.2
Một quan hệ trên tập hợp ? được nói là một thứ tự nếu nó phản xạ, phản xứng và bắc cầu. Khi ấy ta nói ? là một tập hợp sắp thứ tự (hay có thứ tự)
Chú ý:
1. Ta thường ký hiệu một thứ tự bởi ≺. Cặp ( ?, ≺) là một tập hợp có thứ tự.
2. Giả sử ? là một tập hợp con của tập hợp có thứ tự ( ?, ≺). Khi ấy ≺ cảm sinh một thứ tự trên ? một cách tự nhiên: với ?, ? ∈ ?, ta nói ? ≺ ? trong ? nếu ? ≺ ? trong ?.
Ví dụ:
1. ( ?, ≤) là một tập hợp có thứ tự. Thứ tự cảm sinh các thứ tự tự nhiên trên ?, O.
2. Nhắc lại tập hợp ?( ?) ta có quan hệ: ? ≺ ? ⟺ ? ⊂ ?
Khi đó ≺ là một thứ tự trên ?( ?) gọi là thứ tự bao hàm. Ký hiêu ? ⊂ ? sẽ được dùng thay vì ≺
Trên tập hợp ? các dạng mệnh đề, ta định nghĩa ? ≺ ? khi và chỉ khi ? ⟹ ?, nghĩa
? là một hệ quả logic của ?. Rõ ràng quan hệ trên có tính phản xạ và bắc cầu.
Mặt khác nếu ? ⟹ ? và ? ⟹ ? thì ? ?à ? ?ươ?? đươ?? ?o?i? . Do đó nếu ta đồng nhất các dạng mệnh đề tương đương logic thì quan hệ trên trở thành một thứ tự trên ?.
Chính xác hơn, ta thấy quan hệ tương đương logic là một quan hệ tương đương trên ? . Ta có một quan hệ trên tập hợp các lớp tương đương như sau: [ ?] ≺ [ ?] ⟺ ? là hệ quả logic của ?
Khi ấy quan hệ trên vẫn còn là phản xạ và bắc cầu.
Giả sử [ ?] ≺ [ ?] và [ ?] ≺ ?. Khi ấy ? là hệ quả logic của ? và ngược lại, nghĩa là ? và ? tương đương logic. Suy ra [ ?] = [ ?]
Do đó ≺ là một thứ tự trên tập hợp các lớp tương đương của ?.
Ví dụ: Gọi ? là một số nguyên dương. Đặt: ࣯? = { ? ∈ ?/ ?|?}
Trong đó ?|? có nghĩa ? là một ước của n hay n chia hết cho a. Trên ࣯? ta có thể định nghĩa một quan hệ: ? ≺ ? ⟺ ?|?
Khi ấy rõ ràng là phản xạ và bắc cầu Giả sử ? ≺ ? và ? ≺ ?. Ta có: ? = ?? và ? = ?? với ?, ? ∈ ?+
Suy ra
? = ??? ⟹ ?? = 1 ?ì ? > 0
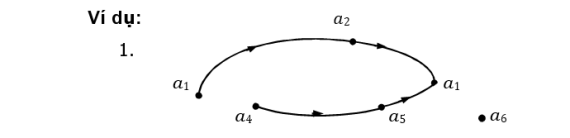
Do ?, ? ∈ ?+ ta phải có ? = ? = 1, nghĩa là ? = ? Quan hệ thứ tự trên vẫn được ký hiệu bởi ?|? Với ? = 12 ta có ࣯12 = { 1,2,3,4,6,12}
Do đó ta có thể liệt kê các cặp thuộc quan hệ trên:
{( 1,1),( 1,2),( 1,3),( 1,4)( 1,6),( 1,12), ( 2,2),( 2,4),( 2,6),( 2,12),( 3,3),( 3,6),( 3,12),( 4,4),( 4,12),( 6,6),( 12,12)}
Tuy nhiên đối với các tập hợp hữu hạn có nhiều phần tử, ta không thể dùng phương pháp liệt kê như trên mà sẽ sử dụng biểu đồ Hasse
Định nghĩa 3.3.3
Xét một tập hợp có thứ tự ( ?, ≺) và ?, ? là hai phần tử bất kỳ của ?
i. Nếu ? ≺ ? ta nói ? là trội của ? hay ? được trội bởi ?
ii. ? là trội trực tiếp của ? nếu ? trội ? và không tồn tại một trội ? của ? sao cho: ? ? ?
Định nghĩa 3.3.4
Biểu đồ Hasse của một tập hợp hữu hạn có thứ tự ( ?, ≺) bao gồm:
i. Một tập hợp các điểm trong mặt phẳng tương ứng 1 – 1 với ?, gọi là các đỉnh
ii. Một tập hợp các cung có hướng nối một số đỉnh: hai đỉnh ?, ? được nói lại bởi một cung có hướng (từ ? tới ?) nếu ? là trội trực tiếp của ?.
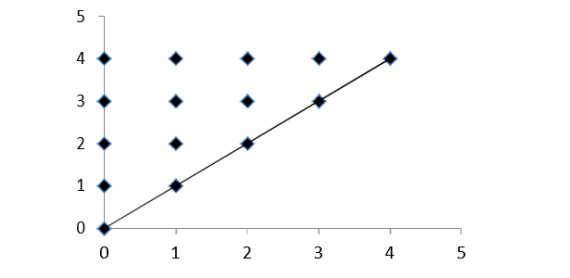
Trên đây là biểu đồ Hasse của tập hợp sắp thứ tự { ?1, ?2, ?3, ?4, ?5, ?6} trong đó:
?1 ≺ ?2 < ?3 và ?4 ≺ ?5 ≺ ?3
?6 không so sánh được với các p hần tử khác, nghĩa là với 1 ≤ i ≤ 5 thì ?6 ⊀ ?i và ?i ⊀ ?6.
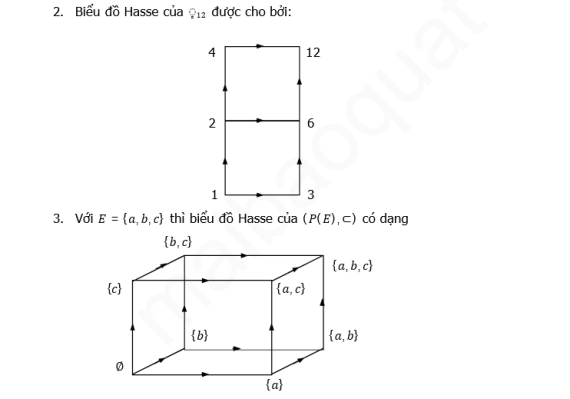
Ở đây ta quy ước các cung là không chéo nhau. Do đó một cách để hình dùng dễ dàng là xem như Biểu đồ Hasse của ?( ?) gồm các đỉnh và cạnh của một hình lập phương 3 chiều.
4. Biểu đồ Hasse của { 1,2,3,4,5} với thứ tự thông thường có dạng một dây chuyền:
Ta có thể duyệt hết các đỉnh một lần bằng cách đi theo các cung mà không quay trở lại
Cũng thế trong vô hạn, ta cũng có thể quy ước biểu diễn thứ tự trên bởi biểu đồ
Biểu đồ Hasse trên vẫn còn là một dây chuyền vô hạn
Định nghĩa 3.3.5
Một thứ tự trên ? được nói là toàn phần nếu hai phần tử bất kỳ đều so sánh được, nghĩa là mệnh đề sau là đúng:
∀?, ? ∈ ?, ( ? ≺ ?) ? ( ? ≺ ?)
Ví dụ:
1. ?, ?, O, ? với thứ tự ≤ thông thường là những tập hợp sắp thứ tự toàn phần
2.Xét một tập hợp hữu hạn không rỗng ? mà ta gọi là bộ mẫu tự. Giả sử trên ? có một thứ tự toàn phần ≺ (ví dụ như thứ tự thông thường nếu ? là bộ chữ cái: ? ≺ ? ≺ ? ≺ ⋯ ≺ ?, hay thứ tự xác định bởi mã ASCII nếu ? là bộ chữ cái được mở rộng thêm các ký tự là các số từ 0 đến 9, các dấu+,-,…)
Gọi ? là tập hợp các chuỗi ký tự có dạng ? = ?1?2 …?? và ?1?2 …?? ∈ ? với ? là số nguyên tự nhiên tùy ý. Với ? = 0 , ta được chuỗi rỗng ∅ không có ký tự nào cả. ta sẽ định nghĩa một quan hệ ≺ trên ? như sau:
- ∅ ≺ ?, ∀? ∈ ?
- Nếu ? = ?1?2 …?? và ? = ?1?2 …?? là hai chuỗi khác ∅, ta định nghĩa ? ≺ ? khi và chỉ khi một trong hai điều kiện sau được thỏa:
i. Tồn tại một chỉ số i, 1 ≤ i ≤ ? sao cho: ?1 = ?1,…, ?i−1 = ?i−1 và ?i ?i
ii. ? ≤ ? và ?1 = ?1,…, ?? = ??
Ta chứng minh được rằng ≺ là một thứ tự trên ? gọi là thứ tự tự điển. Hơn nữa với thứ tự tự điển, ? là một tập sắp thứ tự toàn phần (Bài tập)
Bây giờ với Định nghĩa 3.3.5, nhận xét trên đây về biểu đồ Hasse có thẻ được phát biểu dưới dạng một kết quả tổng quát hơn mà chứng minh là hiển nhiên.
Mệnh đề 3.3.1:
Biểu đồ Hasse của ( ?, ≺) là một dây chuyền khi và chỉ khi ≺ là một thứ tự toàn phần trên ?.
Do Mệnh đề 3.3.1, biểu đồ Hasse của một tập hợp sắp thứ tự toàn phần hữu hạn là một dây chuyền xuất phát từ một phần tử ? và chấm dứt bởi 1 phần tử ?. Rõ ràng ? là phần tử bé nhất và ? là phần tử lớn nhất theo nghĩa: ∀? ∈ ?, ? ≺ ? ≺ ?
Mặt khác, Ví dụ 1 cho thấy phần tử bé nhất và lớn nhất không nhất thiết tồn tại, ngay cả trong 1 tập hợp sắp thứ tự hữu hạn. Tuy nhiên các phần tử ?3, ?6 là những phần tử tối đại và ?1, ?4, ?6 là những phần tử tối tiểu theo nghĩa sau:
Định nghĩa 3.3.6:
Trong tập hợp sắp thứ tự ( ?, ≺) , một phần tử ? được nói là tối đại (tương ứng tối tiểu ) nếu ? không có trội thực sự (tương ứng không là trội thực sự của phần tử nào cả). Nói cách khác mệnh đề sau là đúng:
∀? ∈ ?, ( ? ≺ ?) ⟹ ( ? = ?) (tương ứng ∀? ∈ ?, ( ? ≺ ?) ⟹ ( ? = ?))
Định lý 3.3.2
Trong một tập hợp sắp thứ tự ?, phần tử lớn nhất ?, nếu tồn tại, là phần tử tố đại duy nhất. Suy ra ? cũng là phần tử lớn nhất duy nhất. Kết luận tương tự cho phần tử bé nhất và phần tử tối tiểu.
Chứng minh: Giả sử ? là phần tử lớn nhất và tồn tại ? sao cho ? ≺ ?. Do ? lớn nhất, ta cũng có ? ≺ ?. Do tính phản xứng, ta có ? = ?. Suy ra ? là một phần tử tối đại.
Mặt khác nếu gọi ? là một phần tử tối đại tùy ý, do ? lớn nhất ta có ? ≺ ?. Nhưng ? là tối đại, ta phải có ? = ?. Như thế ? là phần tử tối đại duy nhất và dĩ nhiên cũng là phần tử lớn nhất duy nhất. Kết luận cho phần tử bé nhất và các phần tử tối tiểu được chứng minh tương tự bằng cách đổi chiều các thứ tự (bất đẳng thức).
Sự tồn tại của phần tử tối đại đối với các tập hợp sắp thứ tự hữu hạn được cho bởi:
Định lý 3.3.3
Trong một tập hợp sắp thứ tự hữu hạn thì:
i. Mọi phần tử được trội bởi (tương ứng trội) một phần tử tối đại (tương ứng tối tiểu)
ii. Nếu ? là phần tử tối đại (tương ứng tối tiểu) duy nhất của ? thì ? là phần tử lớn nhất (tương ứng phần tử bé nhất)
Chứng minh:
1. Xét một phần tử ? ∈ ?. Nếu ? không tối đại sẽ có ?1 ∈ ? sao: ? : x x1
Nếu ?1 tối đại thì đó là phần tử phải tìm.
Nếu không sẽ có ?2 ∈ ? sao cho: ?1?2
Nếu ?2 tối đại thì đó là phần tử phải tìm vì ?2 rõ ràng trội ?. Nếu không ta tiết tiếp tục tìm được một trội thực sự của ?2 …
Do ? hữu hạn và các phần tử ?, ?1, ?2,… đôi một khác nhau, quá trình trên sẽ dừng sau tối đa ? − 1 bước, trong đó ? = |?|. Phần tử cuối cùng tìm được chính là phần tử tối đại trội ?.
2. Giả sử ? là phần tử tối đại duy nhất của ?, và ? là một phần tử tùy ý của ?. Do i) tồn tại một phần tử tối đại ? sao cho: ? ≺ ?.
Do ? duy nhất ta có: ? = ?
Suy ra ? ≺ ?, ∀? ∈ ?
Nói cách khác ? là phần tử lớn nhất.
Chứng minh cho kết luận về phần tử tối tiểu và phần tử bé nhất hoàn toàn tương tự.
Chú ý: Nếu ? không hữu hạn, Định lý không đúng theo cả khi kết luận:
1. ? không có phần tử tối đa; ví dụ như ? = ? với thứ tự thông thường.
2. ? có thể có phần tử tối đại duy nhất ? nhưng không có phần tử lớn nhất như ví dụ sau cho thấy:
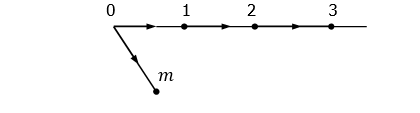
DÀN
Giả sử ? là một tập hợp con hữu hạn của tập hợp sắp thứ tự toàn phần ?, khi ấy phần tử lớn nhất của ? tồn tại và được ký hiệu bởi max ?. Tương tự, phần tử bé nhất của ? tồn tại, và được ký hiệu bởi min ?.
Đối với các tập hợp sắp thứ tự không toàn phần , khái niệm max, min có thể được giảm nhẹ thành khái niệm sup và inf như sau:
Định nghĩa 3.4.1
Giả sử ? là một tập hợp con của tập hợp sắp thứ tự ( ?, ≺). Khi ấy
1. Một phần tử ? ∈ ? được nói là chặn trên (tương ứng chặn dưới ) chung của ? nếu: ∀? ∈ ?, ? ≺ ? (tương ứng ∀? ∈ ?, ? ≺ ?)
2. Phần tử bé nhất (tương ứng lớn nhất) của tập hợp
{ ? ∈ ?/ ? là chặn trên chung của ? } (tương ứng { ? ∈ ?/ ? là chặn dưới chung của ? } ) được ký hiệu bởi sup ? (tương ứng inf ?)
Ví dụ:
1. Trong một tập hợp sắp thứ tự toàn phần ?, rõ ràng max ? của một tập hợp con hữu hạn ? chính là sup ?. Tương tự min ? chính là inf ?.
2. Giả sử ? = { ?1, ?2,…, ??} là một tâp hợp con hữu hạn của ?( ?).
Khi ấy ?i chính là sup ? ?à ?i chính là inf ?
Trên tập hợp ? các dạng mệnh đề với thứ tự ⟹, xét một tập hợp con hữu hạn ℰ = { ?1, ?2,…, ??}. Khi ấy ?1 ? ?2 ? …? ?? và ?1 ? ?2 ? …? ?? chính là sup ℰ và inf ℰ (Bài tập).
Định nghĩa 3.4.2
Một tập hợp sắp thứ tự ( ?, ≺) được nói là một dàn nếu với hai phần tử bất kỳ ?, ? ∈ ?, thì sup { ?, ?} và inf { ?, ?} luôn luôn tồn tại.
Ký hiệu: trong một dàn, ta sẽ ký hiệu sup { ?, ?} và inf { ?, ?} bởi ? ? ? và ? ? ?.
Ví dụ:
1. Một tập hợp sắp thứ tự toàn phần là một dàn
2. ?( ?) với thứ tự bao hàm là một dàn. Ta có:
?1 ? ?2 = ?1 ? ?2
?1 ? ?2 = ?1 ∩ ?2
3. ? với thứ tự ⟹ là một dàn: với ?, ? là hai dạng mệnh đề, các ký hiệu mới ?, ? dành cho sup{ ?, ?} và inf{ ?, ?} trùng với các ký hiệu quen thuộc của phép nối rời và phép nối liền: ? ? ? và ? ? ?.
4. Tập hợp ? = { ?, ?, ?, ?, e, ƒ} với biểu đồ Hasse dưới đây không phải là một dàn vì { ?, ?} không có sup. Thật vậy các trội chung của { ?, ?} là { ?, e, ƒ} và tập hợp này không có phần tử bé.
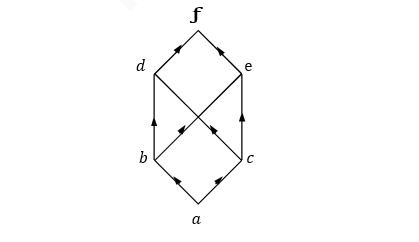
Tương tự ta cũng thấy { ?, e} không có inf.
Định lý 3.4.1
Trong một dàn ( ?, ≺) các phép toán ? và ? thỏa các tính chất giao hoán và kết hợp:
i. ? ? ? = ? ? ? ?à ? ? ? = ? ? ? ∀?, ? ∈ ?
ii. ? ? ( ? ? ?) = ( ? ? ?) ? ? ?à ? ? ( ? ? ?) = ( ? ? ?) ? ? ∀?, ? ∈ ?
Chứng minh:
i) Hiển nhiên nên ta chỉ cần chứng minh ii). Xét 3 phần tử bất kỳ ?, ?, ? ∈ ?. Khi ấy ? = ? ? ( ? ? ?) là một trội chung của ? và ? ? ? nên nó cũng là một trội chung của ?, ? và ? thì ? ? ? ≺ ? vì ? ? ? là trội chung bé nhất của { ?, ?} . Như thế ? là trội chung của { ?, ? ? ?}. Suy ra ? = ? ? ( ? ? ?) ≺ ?.
Như thế ? chính là trội chung bé nhất của { ?, ?, ?}. Tương tự ta cũng thấy ( ? ? ?) ? ? cũng là trội chung bé nhất của { ?, ?, ?}. Do phần tử bé nhất là duy nhất, ta có:
? ? ( ? ? ?) = ( ? ? ?) ? ?
Chứng minh của ? ? ( ? ? ?) = ( ? ? ?) ? ? hoàn toàn tương tự.
Chú ý: Do tính kết hợp, nếu ? = {?1, ?2, …, ??} là một tập hợp con hữu hạn của dàn ? thì ?1 ? ?2 ? …? ?? không phụ thuộc vào cách đặt các dấu “( )”. Hơn nữa, chứng minh tương tự như trong Định lý 3.4.1 ta thấy ?1 ? ?2 ? …? ?? chính là sup ?. Tương tự ?1 ? ?2 ? …? ?? = inf ?. Đặc biệt nếu ? hữu hạn ta có:
Mệnh đề 3.4.2
Trong dàn hữu hạn ? = { ?1, ?2,…, ??} thì ?1 ? ?2 ? …? ?? và ?1 ? ?2 ? …??? chính là phần tử lớn nhất và phần tử bé nhất của ?.
Chú ý: Nếu dàn ? không hữu hạn thì phần tử lớn nhất và bé nhất không nhất thiết tồn tại như ví dụ của ? cho thấy.
Định nghĩa 3.4.3
Một dàn ? được nói là phân bố nếu với mọi ?, ?, ? trong ? ta có:
? ? ( ? ? ?) = ( ? ? ?) ? ( ? ? ?)
?à ? ? ( ? ? ?) = ( ? ? ?) ? ( ? ? ?)
Ví dụ:
1. Mọi tập hợp sắp thứ tự toàn phần là một dàn phân bố (Bài tập)
2. Do tính phân bố của các phép tính tập hợp, dàn ?( ?) là một dàn phân bố.
3. Do quy luật phân bố, dàn ? các dạng mệnh đề là một dàn phân bố
4. Xét tập hợp sắp thứ tự ? = { ?, ?, ?, ?, e} với biểu đồ Hasse như sau:
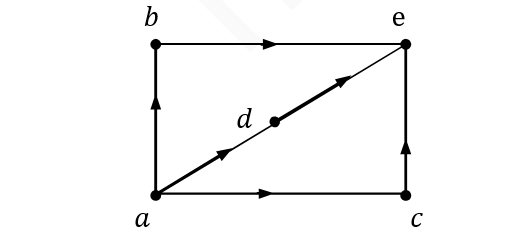
Ta có thể kiểm tra dễ dàng ? là một dàn. Tuy nhiên ? không phân bố vì:
? ? ( ? ? ?) = ? ? e = ?
Trong khi ( ? ? ?) ? ( ? ? ?) = ? ? ? = ? ≠ ?
Định nghĩa 3.4.4
Giả sử ? là một dàn với phần tử lớn nhất mà bé nhất mà ta ký hiêu là 1 và 0. Khi ấy một phần tử ?̅ ∈ ? được nói là phần bù của phần tử ? ∈ ? nếu:
? ? ?̅ = 1
?à ? ? ?̅ = 0
Ta nói ? là một dàn bù nếu mọi phần tử của ? đều có phần bù.
Chú ý: Nếu ?̅ là phần bù của ? thì rõ ràng ? là phần bù của ?̅
Ví dụ:
1. Các dàn ?( ?) và ? là dàn bù. Phần bù của ? ∈ ?( ?) chính là phần bù của tập hợp ? trong ?, còn phần bù của dạng mệnh đề ? chính là phủ định của ?.
2. Dàn ? = { ?, ?, ?, ?, e} với biểu đồ Hasse như dưới đây là một dàn bù
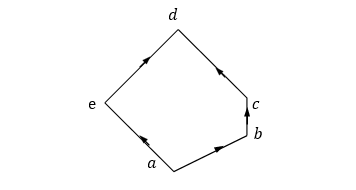 DÀN 2?
DÀN 2?
Cho trước hai tập hợp ?, ?, nhắc lại rằng ?? ký hiệu tập hợp các ánh xạ từ ? vào ?.
Giả sử ≺? là một thứ tự trên ?. Khi ấy với ƒ, ? ∈ ??, ta định nghĩa:
ƒ ≺ ? ⟺ ∀? ∈ ?, ƒ( ?) ≺? ?( ?)
Có thể kiểm tra rằng ≺ là một thự tự trên ??, và hơn nữa ( ??, ≺) là một dàn nếu ( ?, ≺?) là một dàn (Bài tập)
Gọi ƒ, ? là hai phần tử bất kỳ của ??, ƒ ? ? và ƒ ? ? là ánh xạ sao cho với mọi ? ∈ ?:
( ƒ ? ?) ( ?) = ƒ( ?) ?? ?( ?)
?à ( ƒ ? ?) ( ?) = ƒ( ?) ?? ?( ?)
Trong đó ?? và ?? chỉ sup và inf của hai phần tử trong ? đối với thứ tự ≺?
Đặc biệt với ? = { 0,1} , ta được dàn {0,1}? mà ta ký hiệu là 2? . Với ƒ ∈ 2? , đặt ? = ƒ−1( 1). Khi ấy ta có:
Ta nói ƒ là hàm đặc trưng của ?
Hàm đặc trưng của ? được ký hiệu bởi 3Æ. Ta có:
Định lý 3.5.1
Tương ứng ?: ? ⟼ 3Æ là một song ánh giữa ?( ?) và 2?. Hơn nữa với ?1, ?2 là hai tập hợp con tùy ý của ? ta có: ?1 ⊂ ?2 ⟺ 3Æ1 ≺ 3Æ2 ( 3.5.1)
Chứng minh: Trên đây ta đã thấy ? là toàn ánh. Hơn nữa nếu 3Æ1 = 3Æ2 thì :
Như thế ? là một song ánh,
Mặt khác, với ?1, ?2 là hai tập hợp con tùy ý của ?, ta có:
?1 ⊂ ?2 ⟺ (∀? ∈ ?, 3Æ1 ( ?) = 1 ⟹ 3Æ2( ?) = 1); 3Æ1 ≺ 3Æ2
Ta có thể viết lại (3.5.1) như sau: ?1 ⊂ ?2 ⟺ ?( ?1) ≺ ?( ?2)
? là đẳng cấu giữa hai tập hợp con có thứ tự ?( ?) và 2? theo nghĩa sau:
Định nghĩa 3.5.1
Môt đẳng cấu giữa hai tập hợp có thứ tự ( ?, ≺Æ) , ( ?, ≺?) là một song ánh ?: ? ⟷ ? sao cho:
∀?, ?, ( ? ≺Æ ?) ⟺ ?( ?) ≺? ?(y) (3.5.2)
Định lý 3.5.2 : Giả sử ? là một đẳng cấu giữa hai tập hợp có thứ tự ( ?, ≺Æ) và ( ?, ≺?)
i. Nếu ( ?, ≺Æ) và ( ?, ≺?) là hai dàn, thì với ?, ? ∈ ? tùy ý ta có:
?( ? ? ?) = ?( ?) ? ?(y) ( 3.5.3)
và ?( ? ? ?) = ?( ?) ? ?(y) (3.5.4)
ii. Nếu ? là dàn phân bố thì ? cũng là dàn phân bố
iii. Giả sử ? có 0 là phần tử bé nhất và 1 là phần tử lớn nhất. Khi ấy ?( 0) và ?( 1) là phần tử bé nhất và lớn nhất của ?.
iv. Nếu ? là dàn bù thì ? cũng là dàn bù. Hơn nữa nếu ?̅ là phần bù của phần tử ? ∈ ?, thì ?( ?̅) là phần bù của ?( ?) . Nói cách khác ?( ?̅) = ̅?̅(̅?̅)̅.
Chứng minh:
i. Với ?, ? ∈ ? tùy ý, do (3.5.2) rõ ràng ?( ? ? ?) là chặn trên chung của ?( ?) và ?( ?) . Suy ra:
?( ?) ? ?( ?) ≺ ?( ? ?y) (3.5.5)
Mặt khác, cũng do (3.5.2) ?−1(?( ?) ? ?( ?)) và chặn trên chung của ? và ? nên:
? ? ? ≺ ?−1(?( ?) ? ?( ?) )
Do đó
?( ? ? ?) ≺ ?( ?) ? ?(y) (3.5.6)
Từ (3.5.5) và (3.5.6) ta suy ra (3.5.3) Chứng minh của (3.5.4) hoàn toàn tương tự.
ii) , iii), iv) được suy ra dễ dàng từ định nghĩa
Hệ quả: nếu ?, ? là hai tập hợp con tùy ý của ? thì
3Æ?? = 3Æ ? 3? ?à 3Æ∩? = 3Æ3?
trong đó 3Æ3? = 3Æ ? 3? là tích của hai hàm theo nghĩa tự nhiên.
DÀN ट?
Ước số chung lớn nhất và bội số chung lớn nhất
Giả sử ?, ? là hai số nguyên dương, khi ấy số nguyên dương ? được nói là ước số chung của ? và ? nếu ? là ước số của ? và ? là ước số của ?. Khi ấy 0 ≤ ? ≤ min( ?, ?) . Do đó tập hợp của các ước số chung của ? và ? là một tập hợp hữu hạn và tồn tại một phần tử lớn nhất ? gọi là ước số chung lớn nhất của ? và ?. Ta viết: ? = ?????( ?, ?)
Để tìm ước số chung lớn nhất của 2 số nguyên dương ?, ? ta sử dụng thuật toán sau:
Thuật chia Euclide: nếu ? là ước của ?, đặt ?0 = ?. Nếu không ta thực hiên lần lượt các phép chia có dư số:
|
?
|
=
|
??1 + ?1
|
,0 ≤ ?1 < ?
|
|
?
|
=
|
?1?2 + ?2
|
,0 ≤ ?2 < ?1
|
|
?1
|
=
|
?2?3 + ?3
|
,0 ≤ r 3 < ?2
|
|
…
|
…
|
…………………
|
…………………
|
|
?k
|
=
|
?k+1?k+2 + ?k+2
|
, 0 ≤ ?k+2 < ?k+1
|
|
…
|
…
|
…………………
|
……………………
|
Do ? > ?1 > ?2 > ⋯ > ?k > ⋯ ≥ 0, thuật chia sẽ ngưng sau một số hữu hạn bước.
Gọi ??+1 là dư số đầu tiên bằng 0. Ta có:
??−2 = ??−1?? + ??, 0 ≤ ?? < ??−1
??−1 = ?? ??+1 + 0
Định lý 3.6.1
?? là ước số chung lớn nhất của ? và ?. Hơn nữa mọi ước số chung của ? và ? là ước số của ??
Chứng minh: Nếu ? là ước của ? thì ước số chung lớn nhất của ? và ? chính là ? = ?0. Nếu không ?1 > 0. Giả sử ? là ước số chung của ? và ?. Do ?1 = ? − ??1 nên ? cũng là ước số của ?i với 1 ≤ i ≤ ?. Thật vậy, giả sử 1 ≤ ? < ? và ? là ước của ?i với 1 ≤ i ≤ ?. Khi ấy do ?k+1 = ?k−1 − ?k?k+i nên ? cũng là ước của ?k+1. Như thế theo nguyên lý qui nạp, ? là ước của ??. Đặc biệt nếu gọi ? là ước số chung lớn nhất của ? và ? thì ? cũng là ước của ??.
Suy ra ? ≤ ??
Ngược lại, do ??−1 = ????+1 nên ?? là ước của ??−1. Tương tự như trên, dùng nguyên lý qui nạp , ta thấy ?? là ước của ?i với 1 ≤ i ≤ ?. Nhưng ? = ?1?2 + ?2 nên ?? cũng là ước của ?. Cuối cùng do ? = ??1 + ?1, cũng là ước của ?. Như thế ?? là ước số chung của ? và ?.
Suy ra ?? ≤ ?
Tóm lại ? = ??
Định lý 3.6.2
Giả sử ? là ước số chung lớn nhất của ? và ?. Khi ấy tồn tại ?, ? ∈ ? sao cho: ? = ?? + ??
Chứng minh: với ký hiệu như trong Định lý 3.6.1, ta có ? = ??. Như thế:
? = ??−2 − ?? ??−1 = ?1??−2 + ?2 ??−1
Nhưng
??−1 = ??−3 − ??−1??−2
Do đó
? = ?2??−3 + ( ?1 − ?2??−1) ??−2
= ?2 ??−3+?3 ??−2
Bằng Nguyên lý qui nạp tương tự như trên ta cũng chứng minh được tồn tại ?1, ?2,…, ??−1 ∈ ? sao cho:
? = ??−2?1 + ??−1?2
? = ??−1? + ( ??−2 − ??−1?2) ?1
Sử dụng ?2 = ? − ?2?1 ta được:
= ??−1? + ??1
= ?? + ( ??−1??1) ?
= ?? + ??
Định nghĩa 3.6.1
Hai số nguyên dương ?, ? được nói là một nguyên tố cùng nhau nếu ước số chung lớn nhất của chúng bằng 1. Khi ấy ta viết ( ?, ?) = 1
Chú ý: Một số nguyên ? > 1 được nói là số nguyên tố nếu ? không có ước nào ngoài 1 và chinh nó. Nếu ? là số nguyện tố và ? không phải là ước của ? thì ? và ? nguyên tố cùng nhau.
Mệnh đề 3.6.3:
Giả sử ?, ?, ? ∈ ?+ sao cho ? là ước của ?? và ( ?, ?) = 1. Khi ấy ? là ước của ?.
Chứng minh: Do Định lý 3.6.2, tồn tại ?, ? ∈ ? sao cho:
1 = ?? + ??
?o đó
? = ??? + ???
Vì ? là ước của ?? nên ? cũng là ước của ? (ĐPCM)
Mệnh đề 3.6.4
Giả sử ?, ?, ? ∈ ?+ sao cho ( ?, ?) = 1 và ( ?, ?) = 1. Khi ấy ( ?, ??) = 1
Chứng minh: Giả sử ước số chung lớ nhất của ? và ?? là ? > 1. Khi ấy ( ?, ?) = 1 vì nếu không, gọi e là ước số chung lớn nhất của ? và ? ta có e > 1. Rõ ràng e cũng là ước chung của ? và ?. Điều này mâu thuẫn với giả thiết ( ?, ?) = 1. Vậy ( ?, ?) = 1. Do đó theo Mệnh đề 3.6.3 ? là ước số của ?. Điều này mâu thuẫn với giả thiết ( ?, ?) = 1. Do đó ? = 1, nghĩa là( ?, ??) = 1 (ĐPCM)
Một số nguyên ? được nói là bội số chung của hai số nguyên ?, ? nếu ? đồng thời là bội số của ? và ?.
Bổ đề 3.6.5
Cho ?, ?, ? ∈ ?+. Giả sử ? là bội số chung của ?, ? và ( ?, ?) = 1. Khi ấy ? là bội số chung của ??.
Chứng minh: Do ? là bội số của ?, ta có thể viết ? = ?? với ? là số nguyên. Do Mệnh đề 3.6.3, ? là ước số của ?: ? = ?′?, ?′ ∈ ?+. Suy ra ? = ?′?? (ĐPCM)
Định lý 3.6 .6:
Giả sử ?, ? ∈ ?+. Gọi ? là ước số chung lớn nhất của ?, ?. Khi ấy là bội số chung của ?, ?. Hơn nữa mọi bội số chung của ?, ? đều chia hết cho . Suy ra là bội số chung lớn nhất của ? và ?.
Chứng minh: Ta có thể viết với ?, ?
Mặt khác để ý rằng và nguyên tố cùng nhau. Thật vậy gọi e là ước số chung lớn nhất của chúng thì ?e cũng là ước số chung của ? và ?. Suy ra e = 1.
Gọi ? là bội số chung của ? và ?. Áp dụng Bổ đề 3.6.5 cho ta thấy là bội số chung của nên ? là bội số chung của (ĐPCM)
Chú ý: ta ký hiệu bội số chung nhỉ nhất của ?, ? bởi ????? ( ?, ?)
Giả sử ? ∈ ?, ? > 1. Khi ấy nếu gọi ? là ước bé nhất của ? sao cho ? > 1 thì rõ ràng ? là một số nguyên tố. Lại tiếp tục xét ? ta chứng minh được bằng qui nạp rằng ? là tích của một số hữu hạn số nguyên tố. Gộp các thừa số giống nhau lại ta có thể phân tích ? thành thừa số nguyên tố:
? = ??1 ??2 …??? ( 3.6.1)
Mệnh đề 3.6.7: Biểu diễn (3.6.1) là duy nhất
Chứng minh: xét một phân tích ra thừa số nguyên tố khác của ?:
(3.6.2)
Nếu ?1 ∉ { ?1, ?2,…, ??} thì áp dụng thì áp dụng Mệnh đề 3.6.4 nhiều lần ta đi đến kết luận ?1 và ? số nguyên tố cùng nhau. Điều mâu thuẫn này chứng tỏ ?1 ∈ {?1, ?2,…, ??}. Lập luận tương tự cho ?2,…, ??, ?1,…, ?? ta được:
{ ?1, ?2,…, ??} = { ?1, ?2,…, ??}
Đặc biệt ? = ? . Sắp xếp thứ tự lại ?1, ?2,…, ?? ta có thể giả sử ?1 = ?1, ?2 = ?2,…, ?? = ??. Ta sẽ chứng minh ?1 = ?1, ?2 = ?2,…, ?? = ?? bằng qui nạp trên ?
- Nếu ? = 1 thì ? = ??1 = ??1. Suy ra ?1 = ?1
- Giả sử ? > 1. Nếu ?1 < ?1 thì r1 = ? 2 …? ? rõ ràng nguyên tố cùng nhau
Do ?1 − ?1 > 0, ?1 là ước của. Điều mâu thuẫn này chứng tỏ ?1 ≥ ?1. Do ?1 và ?1 đóng vai trò đối xứng ta cũng có ?1 ≤ ?1, nghĩa là ?1 = ?1. Khi ấy ta được 2 biểu điễn của ? thành thừa số nguyên tố:
Áp dụng giả thiết qui nạp ta được ?2 = ?2, ?3 = ?3,…, ?? = ??
Sử dụng phân tích (3.6.1) ta có một phương pháp thứ hai để tìm ước số chung lớn nhất và bội số chung nhỏ nhất của hai số nguyên dương.
Trước tiên nhận xét rằng nếu ? và ? có phân tích
? = ??1??2 …??? (3.6.3)
? = ??1??2 …??? (3.6.4)
Thì ? là ước của ? khi và chỉ khi 2 điều kiện dưới đây được thỏa:
- { ?1, ?2,…, ??} ⊂ { ?1, ?2,…, ??}. Đặc biệt ? ≤ ?
- Ta sắp xếp thứ tự ?1, ?2,…, ?? lại sao cho ?1 = ?1, ?2 = ?2, ?? = ??. Khi ấy các số mũ thỏa: ?1 ≤ ?1, ?2 ≤ ?2,…, ?? ≤ ??.
Chứng minh của khẳng định trên dựa trên cùng ý tưởng với chứng minh Mệnh đề 3.6.7 nêu được dành cho đọc giả.
Bây giờ giả sử ? và ? có phân tích như trong (3.6.3) và (3.6.4) với các số mũ nguyên dương. Bằng cách bổ sung thêm vào ? các thừa số là lũy thừa 0 của những số nguyên tố trong (3.6.3) và ngược lại, ta có thể giả sử ?, ? có dạng:
? = ??1??2 …???
? = ??1??2 …???
Với các số mũ lấy giá trị nguyên dương hay 0. Khi ấy do nhân xét trên ta có:
Mệnh đề 3.6.8
?????( ?, ?) = ??1??2 …???
và ?????( ?, ?) = ??1??2 …???
với ?i = min( ?i, ?i) và ?i = max( ?i, ?i)
Dàn ट?
Nhắc lại rằng tập hợp gồm các ước số dương của ? được sắp thứ tự bởi quan hệ:
? ≺ ? ⟺ ?|? (? là ước số của ?)
Giả sử ?, ? ∈. Khi ấy ? = ?????( ?, ?) ∈ ࣯?
Rõ ràng ? ≺ ? và ? ≺ ?. Hơn nữa nếu ? ∈ ࣯? sao cho ? ≺ ? và ? ≺ ? thì ? là ước số chung của ?, ? nên theo Định lý 3.6.1 ? cũng là ước số của ?, nghĩa là ? ≺ ?.
Nói tóm lại ? chính là inf( ?, ?) . Tương tự ?????( ?, ?) là sup( ?, ?) . Với ký hiệu ?,? cho inf và sup ta có:
? ? ? = ?????( ?, ?)
? ? ? = ?????( ?, ?)
Như thế ࣯? là một dàn phần tử bé nhất là 1, phần tử lớn nhất là ?.
Hơn nữa nếu gọi ?1, ?2,…, ?? là các ước số nguyên tố của ? thì ta có thể biểu diễn 1 phần tử bất kỳ của ࣯? dưới dạng (3.6.1) với số mũ thuộc ?. Xét ba phần tử tùy ý ?, ?, ? ∈ ࣯? với biểu diễn như trên:
? = ??1??2 …???
? = ??1??2 …???
? = ??1??2 …???
Khi ấy do Mệnh đề 3.6.8 số mũ của ?i trong ? ? ( ? ? ?) là:
min( ?i, max(, ?i) ) = max( min( ?i , ?i) , min( ?i , ?i))
Như thế ? ? ( ? ? ?) = ( ? ? ?) ? ( ? ? ?) Tương tự ? ? ( ? ? ?) = ( ? ? ?) ? ( ? ? ?) Tóm lại ta đã chứng minh.
Định lý 3.6.9 ࣯
? là một dàn phân bố.
Một số nguyên dương ? được nói là không có thừa số chính phương nếu ? không chia hết cho bình phương của bất kỳ số nguyên >1 nào.
Định lý 3.6.10: ࣯
? là dàn bù khi và chỉ khi ? không có thừa số phương.
Chứng minh: Giả sử ? không có thừa số chính phương và ? là một phần tử tùy ý của ࣯?. Khi ấy ? và ? nguyên tố cùng nhau vì nếu không, bất kỳ ước số chung ? > 1 của chúng ? cũng đều có bình phương là ước của ?.
Như thế 
? ? = 1
Ngoài ra
? ? = ????? (?, ) = ? = ?
Vậy ? chính là phần bù của ? và do đó là một dàn bù.
Ngược lại, giả sử ? chia hết cho bình phương của số nguyên ?>1. Gọi ?̅ là phần bù của ? trong ࣯?. Ta có:
? ? ?̅ = 1
? ? ?̅ = ?
Mà
? ? ?̅ =
Suy ra ?̅ = ?. Nhưng ? rõ ràng là ước số chung của ? và ? nên ? ? ?̅ ≠ 1.
Điều này mâu thuẫn chứng tỏ ? không có phần bù và ࣯? không phài là một dàn bù. Thật ra trong chương 4 ta sẽ chứng minh rằng nếu có một thứ tự nào đó trên ࣯? để nó trở thành một dàn bù thì số phần tử của ࣯? phải là một lũy thừa của 2. Trong khi đó số ước của ? là một lũy thừa của 2 thì trong phân tích của ? thành thừa số nguyên tố, các số mũ phải có dạng 2? − 1
Tóm tắt lý thuyết toán cao cấp
Tóm tắt lý thuyết toán rời rạc Chương 1: Cơ sở Logic
Tóm tắt lý thuyết toán rời rạc Chương 2: Phương pháp đếm
Tóm tắt lý thuyết toán rời rạc Chương 3: Quan hệ
Tóm tắt lý thuyết toán rời rạc Chương 4: Đại số Bool và hàm Bool
Việc làm dành cho sinh viên:
Việc làm thực tập sinh quản trị cơ sở dữ liệu
Việc làm gia sư các môn cập nhật theo ngày mới nhất
Việc làm thêm nhân viên phục vụ nhà hàng/ quán cafe dành cho sinh viên
Việc làm cộng tác viên kế toán
Mức lương của Thực tập sinh kế toán là bao nhiêu?














